IEEE 754 浮動小数点入門
レイトレ合宿7 アドベントカレンダー 7週目の記事です。
IEEE 754 浮動小数点
IEEE 754 浮動小数点は、本当は完全に扱えるはずもない実数をコンピューター上であたかもそれが実数を扱えるかのような錯覚を感じさせるのに成功している浮動小数点の標準規格です。過去にはたくさんの表現方法があったようですし、新しい表現方法が研究されていたりもするようですが、本記事では浮動小数点はすべて IEEE Standard for Floating-Point Arithmetic のことを指します。
レイトレーシングに限らずコンピューターで浮動小数点を使った数値計算は極めて広い応用がありますが、それにもかかわらず浮動小数点の負の側面、誤差やそれに対する傾向と対策についてはそれほどスポットが当たっていないように思います。 そこで今回はゼロから浮動小数点の扱いについて考えてみようと思います。
内部表現
浮動小数点を理解するには、やはりまずその表現について把握することから始めるのが良いでしょう。 浮動小数点の内部表現といっても、何ビットで表現するか?という問題があります。最も一般的なのは、32bitのbinary32, 64bitのbinary64でしょうか。C++ならそれに対応するのがfloat, doubleというのは極めて身近なデータ型でしょう。しかしC++はIEEE 754 浮動小数点が使われているかは処理系定義であることは注意が必要ですが、実際はそのように仮定しても問題ない環境は多いのではないでしょうか。ここではわかりやすさのため、binary32を仮定して話を進めます。テストコードについてはC++で行います。
binary32では浮動小数点は以下のように定義されます。
ここで は符号部で 0 か 1 の1bit 、
は二進数の仮数部で、Mが23bitつまり23桁あります。
Eは指数部で0から255、つまり8bitです。
wikipediaの図にするとビットの格納方法が一目でわかって便利です。
 ※https://ja.wikipedia.org/wiki/IEEE_754 より
※https://ja.wikipedia.org/wiki/IEEE_754 より
...これで浮動小数点を完全に理解できるならばどんなに幸せでしょうか。しかしあきらめずに少しずつ紐解いていくことにします。
仮数部
先立って仮数部については簡単に補足します。仮数部は知っての通り、

のように10進数と対応します。ただしこの図では整数の部分が11の例ですが、浮動小数点では一番左は 1. となる決まりであり、0.とか11.とかはありえません。1つの理由としては、例えば 0.000001 を表現するのに左側のゼロ6個に6ビットつかうのはやはり無駄だからです。せっかく指数部があるのですから、小数点の位置を右に6回動かしてしまえば一番左は 1. になり、もしさらに右に桁があった場合には無駄なく使うことができます。
さらに1. が固定ならば、そこを除いて格納すれば節約になります。というわけで という表現になっています。ここで
はどんな数かを少し考えてみます。最初に仮にMが4桁で[M=1010]だったとすると、
ということは、binary32ではMは23桁であるので、
という数だということがわかります。 ということは、仮数部の項というのは、どうやらMをいじくると1以上2未満の間を行ったり来たりできることがわかります。
指数部
指数部は二進小数点の点の位置を移動させていると先に述べました。しかしこれだけではあまり脳内にイメージできないかもしれません。 そこで数値が与えられたときどのような指数を持つのかを簡単に実験してみます。 実験に先立ってfloatとuint32を相互変換できると便利ですので、以下の関数を準備します。
inline uint32_t as_uint32(float f) {
return *reinterpret_cast<uint32_t *>(&f);
}
inline float as_float(uint32_t u) {
return *reinterpret_cast<float *>(&u);
}
※ unionを使った再解釈は、C++では未定義動作とのことです
そして以下の関数で指数部を取り出してみます。
inline uint8_t get_exponent(float f) {
uint32_t e = as_uint32(f) & 0x7F800000;
return e >> 23;
}
-10から10くらいの間で浮動小数点を生成して、値をx、 すなわち 指数部が2の何乗であるか? を y にしてプロットしたものが以下の図になります。格子の大きさは1です。

xが 0から1のエリアを見てみると、指数は0になっています。つまり、
右隣はどうでしょうか?2から4のエリアです。
なるほど、確かに式の通りです。左隣の0.5から1のエリアはどうでしょうか?
元の範囲が1から2であるため、2倍もしくは1/2倍にしていけば確かに領域を重なることなく埋め尽くすことができます。 なるほどよく考えられているものです。

このことから、指数部というのは担当領域、ある種窓のようなものだと捉えることができるわけです。
再び仮数部へ
指数部によって担当領域が決まること、そしてその幅が可変であることを確認しました。一方で仮数部の項は範囲が固定されているのも確認しました。
ここで表現できる数の精度限界について考えてみます。指数部と符号はあくまでも範囲を決めているわけなので、精度について重要なのはやはり仮数部になります。浮動小数点の定義から考えると、指数部で決まった範囲を仮数部が均等に刻んでいる、と捉えることができます。
例えばMが2ビットだった場合は、以下のように範囲が刻まれるでしょう。

実際にはbinary32では23ビットであるため、区間は 個に分割されることになります。
ということは、例えば1から2の区間の長さは1であるため、最小幅は、
となることがわかります。この数は特別に、”1より大きい最小の数”と1との差、として計算機イプシロン、もしくはマシンイプシロンと呼ばれています。ここでは https://github.com/catchorg/Catch2 を使って簡単なテストとして書いてみると、
TEST_CASE("machine_epsilon") { REQUIRE(std::ldexp(1.0f, -23) == std::numeric_limits<float>::epsilon()); }
と、このように実験で確認することができます。
しかし実際には指数部によって定義される区間の幅は可変長であるため、この最小幅も可変であることに気づきます。そこである数を絶対値が大きくなる方向へ1歩だけ動かす最小幅はどんな数であるか考えると、ある数のMを1インクリメントしたときの差分を考えればよさそうです。
ここで、が、
であったのを思い出して、
とてもシンプルになりました。そしてこの数をulp(unit in the last place) と呼びます。仮数部の最小の桁の単位という気持ちですね。
しかしこの式は浮動小数点の内部表現のに強く依存しており、若干泥臭いです。そこで少し違うアプローチで表現することを考えます。
ulpと似た概念でufp(unit in the first place)というのがあります。それは、
ここで、は床関数になります。
これは何かというと、xの値の、指数部が定義する範囲の幅を表しています。

ということはulpは、その範囲の幅が仮数部によって分解された1つであることから、以下の式で定義できます。
※ aは0でないとします。
このようにEの代わりに数値そのものと結びつけた表現として扱うこともできます。ついでにいうと左の項は計算機イプシロンになっていますね。
ここである実数 を最も近い浮動小数点に丸める関数を
とすると、丸めたときの誤差は、
が満たされることになります。ulpを使わない表現としては、
があり、このとき、
のuを単位相対丸め、という名前で使われることがあります。24は仮数部の桁数でもあるので、これをpとして、
と表現されることもあります。これを使うと先の式は、
となります。ただし、計算機イプシロンとは違う値になるので、注意が必要です。例えば、GDC Vault - Math for Game Developers: Understanding and Tracing Numerical Errors in C++ ではその点に間違いがあったりします。※もちろんこれはこれで良い資料です。
以下は範囲とulpを表にしたものです。特筆すべき点としては、16777216以上ではもうulpが2以上になるため、もはや整数であっても表すことができない数字がここから出始めています。16777216は32bit整数型ではまだ全然余裕があることを考えると、これはかなりのデメリットです。
また、この表では指数関数的にulpが拡大するようにも見えますが、範囲も指数関数的に広がっているので、実際には表す数字とulpは比例関係(もちろん飛び飛びですが)になっていることには注意しましょう。
ゼロにならない?
浮動小数点の定義より、0に近い数字を表すためにはEにできるだけ小さな値を設定すれば良さそうです。そんなわけで最小値は、
この値は大体、
なので、かなり0に近いは近いのですが、0ではありません。さらに問題なのは0までの距離です。E=0付近を図にすると、

と
の間は仮数部により細かく刻まれていることを思い出すと、この0までの距離は
倍もの大きさの隙間であり、マイナスも考えると、その2倍の隙間が0の場所で存在することになります。そう考えると、これを無視するわけにはいきません。
非正規化数
そんなわけで、浮動小数点では、E=0のときだけ定義を変えてしまおう、ということになっています。それは以下の定義です。
違いはわずかですが、最初の定義では最小の区間は、
という区間でしたが、新しい定義では、
そう、なんてことはない、0にもっとも近い部分の範囲だけ特別に0まで引き伸ばしているというわけです。

この特殊化された状態にある浮動小数点を、非正規化数と呼び、最初の定義のほうを正規化数と呼びます。
これなら、0は、 で表すことができます。
0付近でいきなり"穴"ができるのも防ぐこともできています。しかしいいことばかりではありません。代償は特殊化による演算パフォーマンスの低下であり、もしも非正規化数の取り扱いを辞めてもそれほど最終結果に影響が出ないと判断できる場合は、非正規化数になったとき0にフラッシュするようなモードを使ってこのパフォーマンス低下を回避することも考えられます。例えばembreeではそれをstrongly recommendedとしています。
https://www.embree.org/api.html#performance-recommendations
FLT_MIN, std::numeric_limits::min()
ところで FLT_MIN, std::numeric_limits
ですので、
TEST_CASE("FLT_MIN") { REQUIRE(FLT_MIN == encode(PLUS_SIGN_BIT, 1, 0)); REQUIRE(std::numeric_limits<float>::min() == encode(PLUS_SIGN_BIT, 1, 0)); REQUIRE(std::numeric_limits<float>::min() == std::ldexp(1.0f, -126)); }
といったコードで確かめることができます。これは名前から勘違いしやすいところです。
-0 と +0
0近傍の話のついでに、0の符号についてついでに確認します。先の話では、0は、 で表すことができると述べました。この時実は符号は 0のときと1のときが存在します。これが-0 と + 0です。例えばcopysignといった関数ではちゃんと符号が反映されます。
TEST_CASE("plus_zero, minus_zero") { REQUIRE(-1.0f == std::copysign(1.0f, -0.0f)); REQUIRE(+1.0f == std::copysign(1.0f, +0.0f)); }
注意しなければならない点としては、数としてはやはり0であることから、-0と+0はバイナリとして一致しないにもかかわらず、==で比較するとtureになるということです。
TEST_CASE("special_cases") { REQUIRE(-0.0f == +0.0f); }
そしてこのことは大なり小なりでもそのように動作します。
TEST_CASE("special_cases") { REQUIRE(+0.0f >= -0.0f); REQUIRE(+0.0f <= -0.0f); REQUIRE((+0.0f < -0.0f) == false); REQUIRE((+0.0f > -0.0f) == false); }
これは例えば、
float x = -0.0f;
if (0.0f <= x) {
printf("%f is positive number?\n", x);
}
if (x <= -0.0f) {
printf("%f is negative number?\n", x);
}
というコードを試してみると、以下のような出力になってしまいます。
-0.000000 is positive number? -0.000000 is negative number?
上のif文は排他的ではなかったのです。 これはややエッジケースすぎる例かもしれませんが、意外と気づかれていないことかもしれません。
memset(&x, 0, sizeof(x));
ところでfloatやdoubleをmemsetなどでbitを全部0で埋めたらどうなるでしょうか? その場合は当然ですから、結局値は+0です。
float x;
memset(&x, 0, sizeof(x));
printf("%f\n", x); // 0.000000
このあたりも良く考えられていて、驚かされます。
例外的な数
のときの特殊化の話をしましたが、
のときも特殊化があり、それは-INF, +INF, NANです。
| S | E | M | |
|---|---|---|---|
| 0 | 255 | 0 | +INF |
| 1 | 255 | 0 | -INF |
| 0~1 | 255 | non 0 | NAN |
ただ、これについては今回はこれ以上踏み込みません
ulpを手に入れる
0付近の話が整理できたので、一度ulpの話に戻ることにします。floatのある数が与えられたとき、そのulpが欲しいときにはどうすればよいでしょうか。といってもさっきの議論によって、
であることがわかっているので、これを実装すると、
const uint32_t MAX_FRACTION = 0x7FFFFF; const bool PLUS_SIGN_BIT = false; const bool MINUS_SIGN_BIT = true; inline float encode(bool signbit, uint8_t expornent, uint32_t significand) { FT_ASSERT(significand < 0x800000); return as_float((signbit ? 0x80000000 : 0) | (static_cast<uint32_t>(expornent) << 23) | significand); }
inline float ulp_only_normal_number(float f) {
int32_t e = get_exponent(f);
return encode(PLUS_SIGN_BIT, std::max(e - 23, 1), 0);
}
ここで問題なのは、正規化数の範囲では、1が最小であり、
を満たさなければなりません。これは結局、
の数のulpだけが正規化数で表現できることを意味します。しかし非正規化数が使えるなら話は別です。非正規化数での表現を見つけるには、
を解いてMを求めれば良さそうです。
求まりました。 というわけで、実装は以下のようになります。
inline float ulp(float f) {
int32_t e = get_exponent(f);
if (24 <= e) {
return encode(PLUS_SIGN_BIT, e - 23, 0);
}
return encode(PLUS_SIGN_BIT, 0, 1 << std::max(e - 1, 0));
}
e-1にmaxが必要なのは、非正規化数のulpを考えるときです。しかし非正規化数のulpはのときのulpと同じであることは、

図から明らかです。したがって、maxでガードすれば良いということになります。"floatのulpはfloatで表現することができる"、というわけですね。
floatの隣の数
実数には隣の数はありませんが、floatには隣の数があります。今までの議論から、あるfloatの数の隣の数が欲しいとき、仮数部の数値を増やしたり減らしたりすれば手にはいりそうですが、仮数部がオーバーフローやアンダーフローすることがあります。ところがここでfloatの内部表現を再確認すると、
 ※https://ja.wikipedia.org/wiki/IEEE_754 より
※https://ja.wikipedia.org/wiki/IEEE_754 より
指数部が仮数部の上位ビットとして存在しています。ということは全体を整数として解釈するならば、仮数部がオーバーフローやアンダーフローしても、自動的に指数部がインクリメント・デクリメントされるだけであることに気づきます。つまり隣の数が欲しければ整数として解釈してインクリメント・デクリメントしても良いということです。
ただ残念なことに、正のfloatは良いのですが、負のfloatの場合はインクリメントすると絶対値が大きくなる方向に進みますが、一方intをインクリメントすると、絶対値は小さくなります。この対応が逆であることは注意しなければなりません。
※ただ、正の値のみを考えれば良い問題も多いので、状況によってこのことは無視できます。
この点に注意しながら、floatを順序づけされたintと相互変換する関数を考えてみます。
inline int32_t to_ordered(float f) {
uint32_t b = as_uint32(f);
uint32_t s = b & 0x80000000; // sign bit
int32_t x = b & 0x7FFFFFFF; // expornent and significand
return s ? -x : x;
}
inline float from_ordered(int32_t ordered) {
if (ordered < 0) {
uint32_t x = -ordered;
return as_float(x | 0x80000000);
}
return as_float(ordered);
}
これを使うと、floatを任意の歩数だけ移動させる関数は、
inline float next_float(float x, int move) {
return from_ordered(to_ordered(x) + move);
}
と簡単に実装できます。
ただこの実装では-0.0と+0.0は両方とも 0にマッピングされてしまうところは注意が必要です。ただこれはメリットでもあります。なぜなら-0の次の数は+0ではなく、 の数であるべきだからです。これは標準の関数である std::nextafter の挙動もそうなっています。もし-0の次が+0だと、数として全く進んでいないことになります。
TEST_CASE("nextafter") { REQUIRE(std::nextafter(-0.0f, +std::numeric_limits<float>::max()) != +0.0f); REQUIRE(std::nextafter(-0.0f, +std::numeric_limits<float>::max()) == (-0.0f + ulp(-0.0f))); }
floatの順序性の応用
それって本当に便利なの?という人もいるかもしれません。なので一つここで応用例を挙げます。例えばOpenCLではfloatに対してatomic な max関数がありません。しかし一方で、uintやintに対してはatomic maxが用意されています。
したがって、先のto_ordered関数を使ったり、もし扱う数がすべて正の数に限定できればもっと単純にuintとしてatomic_maxを使っても結果的に正しく処理できるはずです。私独自のラッパーを使っており、少し読みにくいかもしれませんが、例えば以下のようになります。
__kernel void find_max(__global float *values, __global uint *max_value) { __local uint local_max; if(get_local_id(0) == 0) { local_max = 0; } barrier(CLK_LOCAL_MEM_FENCE); float value = values[get_global_id(0)]; atomic_max(&local_max, as_uint(value)); barrier(CLK_LOCAL_MEM_FENCE); if(get_local_id(0) == 0) { atomic_max(max_value, local_max); } }
TEST_CASE("max_value") { using namespace rt; auto &env = OpenCLProgramEnvioronment::instance(); env.setSourceDirectory("../kernels"); rt::Xoshiro128StarStar random; OpenCLContext context; int deviceCount = context.deviceCount(); for (int device_index = 0; device_index < deviceCount; ++device_index) { // INFO("device name : " << context.device_info(device_index).name); auto lane = context.lane(device_index); OpenCLProgram program("find_max.cl", lane.context, lane.device_id); OpenCLKernel kernel("find_max", program.program()); for (int j = 0; j < 100; ++j) { std::vector<float> values; for (int i = 0; i < 1000; ++i) { values.push_back(random.uniform(0.0f, 1000.0f)); } float min_value_truth = 0.0f; for (auto f : values) { min_value_truth = std::max(min_value_truth, f); } OpenCLBuffer<float> values_gpu(lane.context, values.data(), values.size(), rt::OpenCLKernelBufferMode::ReadWrite); float min_value = 0.0f; OpenCLBuffer<uint32_t> min_value_gpu(lane.context, (uint32_t *)(&min_value), 1, rt::OpenCLKernelBufferMode::ReadWrite); kernel.setArguments(values_gpu.memory(), min_value_gpu.memory()); kernel.launch(lane.queue, 0, values.size()); min_value_gpu.read_immediately((uint32_t *)(&min_value), lane.queue); REQUIRE(min_value == min_value_truth); } } }
※0以上を仮定しています
このようなハックが可能なのは内部表現の規則のおかげです。
整数
浮動小数点は誤差がある、誤差に気をつけなさい、と耳にタコができるくらいに聞きすぎると、整数の演算にも丸め誤差などが入り込むような錯覚を覚えることがあるかもしれません。 しかし仮数部はbinary32の場合二進数で24桁あり、この範囲では丸め誤差なく完全に表現することができます。
※仮数部は、 となっているためビット数よりも桁が一つ多いです
1100110......10. [ 24桁 ]
せいぜい23歩程度の小数点の移動であり、指数部のビットが足りなくなることもありませんね。24桁ですべて1なら、16777215になります。しかし、 であるため、-16777216から16777216までが完全に表現できる最大ということになります。16777217は残念ながら表現できません。ulpが2だからです。この範囲であれば例えば、
int x = -16777216; /* 2^24 */
for (float i = x; i <= 16777215.0f /* 2^24 - 1 */; i += 1.0f) {
REQUIRE(i == x);
++x;
}
REQUIRE(x == 16777216);
は意図通りに動作します。このように整数をちゃんと表せることが、JavaScriptの数値は64ビットの浮動小数点数だけ、というのを正当化する一つの理由となっています。
誤差
誤差については今まで真の値を丸めたときの誤差しか触れていませんでした。浮動小数点演算では誤差が発生する、と多くの人は認識しており、floatの比較には気を付けましょう、といったことや、答えが0に近づく引き算をしない、などのTipを聞くことはよくあります。有名な既存手法としては、以下のものがあります。
区間演算
floatやdoubleや、より高価な演算を使っても誤差が出るものは出る。ならば正確な答えを出すことよりも、正確な答えのある範囲を確実に求めよう、というのが区間演算のアイディアです。IEEE 754 浮動小数点では四則演算とsqrtは、無限の精度で計算され、それが丸められて答えになるように定められている事実を利用して、精度の保証を行います。
エラーフリー変換
を、なにかの演算を無限の精度で行ってそれを浮動小数点に丸める計算だとします。多くのシチュエーションでは、
のように丸め誤差のために浮動小数点で真の値を得ることができません。しかし、
ここでxはなるべく絶対値が大きな数、yは絶対値がなるべく小さい数です。このような変換ができることが知られています。これを利用してあたかも倍の精度で演算が行えるような計算手法が提案されています。
あたかも倍の精度の演算が行えることから double-double演算とも呼ばれるそうです。カハンの加算アルゴリズムもこの手法にアイディアは似ています。
しかし残念ながらこれらの手法はどのように計算をどのように改善すれば良いか?に直接答えてくれるわけではありません。なのでここでは紹介にとどめます。
Practically Accurate Floating-Point Math
そこで、既存の計算アルゴリズムをどのように改善したらよいのか?という視点では、
Neil Toronto and Jay McCarthy | Brigham Young University, "Practically Accurate Floating-Point Math"
が大変よくまとまっており、有益だと感じました。そこで今回はこちらを紹介したいと思います。
エラーの定義
まずはエラーとはどういうものかを定義します。
ここでxは誤差があるかもしれない浮動小数点数、rは真の値です。真の値から何ulpずれているのか?というのがエラーである、というわけです。ulpは相対的な値ですから、相対誤差にも近い概念です。
例えば以下のような関数でいつでも評価できるようにすると便利です。
template <class T>
float flulp_error(float x, T r) {
T e = (T(x) - r) / T(ulp(float(r)));
return std::fabs(float(e));
}
Racketではリファレンスとなる値の計算のためにMPFRを使っているそうです。今回私はwindows, C++の環境のため、vcpkg から、
vcpkg install mpfr:x64-windows vcpkg install mpir:x64-windows
を入れたあと、boost::multiprecision を使います。
using namespace boost::multiprecision;
using Real = mpfr_float_1000;
printf("%f\n", flulp_error(next_float(1.0f, 4), Real(1.0f))); // 4.000000
このように使うことができます。 ほかにも例えばfloatのexpについて調べたい場合、
using namespace std;
using namespace boost::multiprecision;
printf("%f\n", flulp_error<mpfr_float_1000>(exp(10.0f), exp(mpfr_float_1000(10.0f)))); //
この例では実行すると0.486941が得られます。これは0.5を超えないため、なかなかいい感じではないでしょうか。無限の精度で演算した後に丸められたとしても、0.5ulpはずれるのは回避できないからです。
floatを調べるのにdoubleはリファレンスとして使えるか?
floatよりもdouble, doubleよりもlong doubleで計算したものをリファレンスとするのは、おそらく多くのケースでうまくいくでしょう。しかし反例もあります。
以下の関数があり、 の時の値を求めます。
これをC++で組むと、
template <class T> T f(T x, T y) { auto x2 = x * x; auto y2 = y * y; auto y4 = y2 * y2; auto y6 = y4 * y2; auto y8 = y4 * y4; return (T(333.75) * y6 - x2 * y6) + x2 * (T(11.0) * x2 * y2 - T(121.0) * y4 - T(2.0)) + T(5.5) * y8 + x / (T(2.0) * y); }
そして、型を変えながら実行してみます。
float a = 77617.0f;
float b = 33096.0f;
printf("%.30f, float (8)\n", (float)f<float>(a, b));
printf("%.30f, double (15)\n", (float)f<double>(a, b));
printf("%.30f, mpfr (30)\n", (float)f<number<mpfr_float_backend<30> >>(a, b));
printf("%.30f, mpfr (50)\n", (float)f<mpfr_float_50>(a, b));
printf("%.30f, mpfr (100)\n", (float)f<mpfr_float_100>(a, b));
printf("%.30f, mpfr (1000)\n", (float)f<mpfr_float_1000>(a, b));
すると、以下の出力が得られました。
1.172603964805603027343750000000, float (8) 1.172603964805603027343750000000, double (15) 1.172603964805603027343750000000, mpfr (30) -0.827396035194396972656250000000, mpfr (50) -0.827396035194396972656250000000, mpfr (100) -0.827396035194396972656250000000, mpfr (1000)
※ 括弧の中は10進数での桁数
驚くべきことに、long doubleまで上げても、変化がないので真実かと思いきや、さらに精度を上げていくと突然符号が変化します。ちょっと作為的な例ですが、浮動小数点の信用ならないふるまいを垣間見ることができます。これはRumpの例題というらしいです。"測定"を何度も行って真実を見極めるのは科学として自然なことですが、数値計算でも条件を変えて色々な角度から観察することは有効ではないでしょうか。
エラーの伝播
何か新しい関数を実装するには、多くの場合、浮動小数点の既存の演算を組み合わせて行われます。ある関数が、もし無限の精度で中間の演算が行われ、最後だけ丸められるとしたらその関数は最大でも0.5ulpの誤差しか生まない極めて理想的な関数であると言えます。しかしながら現実的にはパフォーマンス上の問題もありすべての関数をそのように組み立てるのは困難です。一方で演算→丸め→演算→丸め→演算→丸め→...を繰り返しているとどんどん誤差は蓄積していき、最終的には演算の意味消失まであり得ます。青天井です。ではどこで誤差は拡大するのでしょうか?
これを観察するために、もし入力値に1ulpの誤差があったとき、結果にどの程度影響するのか?を以下のようにテストしてみます。
printf("%f\n", flulp_error<mpfr_float_1000>(log(next_float(1.1f, 1)), log(mpfr_float_1000(1.1f)))); // 14.302301
もうちょっと0に近づいてみます。
printf("%f\n", flulp_error<mpfr_float_1000>(log(next_float(1.01f, 1)), log(mpfr_float_1000(1.01f)))); // 126.738930
さらに
printf("%f\n", flulp_error<mpfr_float_1000>(log(next_float(1.0001f, 1)), log(mpfr_float_1000(1.0001f)))); // 16382.376953
入力値が1に近づけば近づくほど、爆発的にエラーが増加しているのがわかります。これはちょうどx軸との交点、結果が0に近づく場所ですね。

これは結局、入力値に1ulpの誤差が含まれただけで、結果の下位ビットの多くの桁が無意味化するということです。これは計算を組み合わせるときに大いに問題になります。ただしこれはあくまでも入力値に誤差が含まれた時の話です。もし入力値が真実に十分近ければ問題にならないこともあります。例えば以下のように
printf("%f\n", flulp_error<mpfr_float_1000>(log(1.1f), log(mpfr_float_1000(1.1f))));
printf("%f\n", flulp_error<mpfr_float_1000>(log(1.01f), log(mpfr_float_1000(1.01f))));
printf("%f\n", flulp_error<mpfr_float_1000>(log(1.0001f), log(mpfr_float_1000(1.0001f))));
// 0.302301
// 0.261070
// 0.377019
全然問題ありません。伝播のしやすさともともとの関数の精度はまったく関係がないのです。 また、時々桁落ちの誤差の説明で、以下のような説明を目にします。
1.3334-1.3333 を計算したいが、答えは 0.0001 になってしまい、有効数字が5桁から1桁に減少する。
なんだか狐につままれたような感じがします。はっきりしているのは、もしもこの二つの入力値が真実なら、答えの0.0001はやはり真実だということです。実際、問題は入力値が丸め誤差などによって信頼できない場合です。
例えば真実の下位の桁が [ ] のような数だったとすると、
1.3334 [ 439475 ] - 1.3332 [ 635621 ] = 0.0001803854
最後に丸めても、
0.00018039
このように最終結果に本来反映されるべきは [ ] の中だったわけで、真実にかなり近い数を保持できるポテンシャルがありながら、丸められた入力値で計算したことで 0.0001のさらに下の桁が失われてしまったわけです。
伝播は誰の仕業か?
ところでこの伝播はどこで拡大するのでしょうか?いったんエラーの定義を確認します。
ここでulpは以下のように近似できると仮定します。
このとき、入力値の 1 ulpのずれを観察します。
ここで、
と捉えると、
これを微分として解釈してしまうと、
最後に浮動小数点丸めを見なかったことにしてもさほど影響がないので無視すると、
ここからわかることは、このエラーの伝播の性質というのは浮動小数点の問題ではなく、本来その関数が持つ性質であったということです。逆に考えると、エラーの伝播のしやすさは、計算アルゴリズムを工夫しても改善できるものではないということです。我々ができるのは、エラーの伝播&拡大しやすいところになるべく立ち入らず、立ち入る場合は誤差をなるべく少なくした状態で入るようにする、といったことなのです。
バッドランド
エラーの伝播&拡大しやすいところを把握することは重要です。Neil Toronto and Jay McCarthy | Brigham Young University, "Practically Accurate Floating-Point Math" では、
の領域を、エラーの伝播&拡大のしやすいところとし、バッドランド(badlands)と呼んでいます。荒地、などと呼んでもいいかもしれませんが、逆にわかりにくい気がするのでカタカナで呼びます。
例えば先のlogのバッドランドを見てみます。gnuplotは割と使いやすいです。
class GNUPlot2D { public: GNUPlot2D() { _fp = std::shared_ptr<FILE>(_popen("gnuplot", "w"), _pclose); gnu_printf("$data << EOD\n"); } void add(double x, double y) { gnu_printf("%f %f\n", x, y); } void show(const char *label, double zMin, double zMax) { gnu_printf("EOD\n"); gnu_printf("set grid\n"); gnu_printf("set yrange[%e:%e]\n", zMin, zMax); gnu_printf("plot '$data' using 1:2 with lines title '%s'\n", label); flush(); } private: void gnu_printf(const char *format, ...) { va_list ap; va_start(ap, format); vfprintf(_fp.get(), format, ap); va_end(ap); } void flush() { fflush(_fp.get()); } std::shared_ptr<FILE> _fp; };
GNUPlot2D p;
int N = 1000;
for (int i = 0; i < N; ++i) {
float x = glm::mix(0.0f, 2.0f, float(i) / N);
float e = flulp_error<mpfr_float_1000>(log(next_float(x, 1)), log(mpfr_float_1000(x)));
p.add(x, e);
}
p.show("log", 0.0, 100.0);

x が1に近い所でバッドランドが観測できます。また、desmosのようなツールを使ってバッドランドを確認するのも良いでしょう。

ちなみにlogの場合は、バッドランドの定義より、解析的に範囲を求めることができます。
続いて、桁落ちの原因とされる x - y のバッドランドも見てみましょう。
class GNUPlot3D { public: GNUPlot3D() { _fp = std::shared_ptr<FILE>(_popen("gnuplot", "w"), _pclose); gnu_printf("$data << EOD\n"); } void add(double x, double y, double z) { gnu_printf("%e %e %e\n", x, y, z); } void next_row() { gnu_printf("\n"); } void show(const char *label, double zMin, double zMax) { gnu_printf("EOD\n"); gnu_printf("set pm3d\n"); gnu_printf("set cbrange[0:8]\n"); gnu_printf("set palette defined(-1 \"blue\", 0 \"white\", 1 \"red\")\n"); gnu_printf("set ticslevel 0\n"); gnu_printf("set zrange[%e:%e]\n", zMin, zMax); gnu_printf("set xlabel 'x'\n"); gnu_printf("set ylabel 'y'\n"); gnu_printf("splot '$data' using 1:2:3 w pm3d title '%s'\n", label); flush(); } private: void gnu_printf(const char *format, ...) { va_list ap; va_start(ap, format); vfprintf(_fp.get(), format, ap); va_end(ap); } void flush() { fflush(_fp.get()); } private: std::shared_ptr<FILE> _fp; };
GNUPlot3D p;
int N = 64;
for (int i = 0; i < N; ++i) {
float y = glm::mix(-1.0f, 1.0f, float(i) / N);
for (int j = 0; j < N; ++j) {
float x = glm::mix(-1.0f, 1.0f, float(j) / N);
float value = next_float(x, 1) - next_float(y, -1);
mpfr_float_1000 truth = mpfr_float_1000(x) - mpfr_float_1000(y);
float e = flulp_error<mpfr_float_1000>(value, truth);
p.add(x, y, e);
}
p.next_row();
}
p.show("x - y", 0.0, 16.0);

0付近は値が大きいので飛んでしまっていますが、xとyが近い値のとき、バッドランドになっていることがわかります。 他にも Neil Toronto and Jay McCarthy | Brigham Young University, "Practically Accurate Floating-Point Math" で既にプロットされたものがあるので、覗いてみるのも良いでしょう。
また、便利なバッドランドリストもあります。
 ※ Figure 6 Neil Toronto and Jay McCarthy | Brigham Young University, "Practically Accurate Floating-Point Math"
※ Figure 6 Neil Toronto and Jay McCarthy | Brigham Young University, "Practically Accurate Floating-Point Math"
関数を改善する
今までの知識を用いて、以下の関数を考えます。ただし簡単のため、x, yは正の数とします。
まずはこれがどれだけの精度があるのかを確認してみます。
float f(float x, float y) { return log(x / y); } mpfr_float_1000 f_truth(mpfr_float_1000 x, mpfr_float_1000 y) { return log(x / y); }
GNUPlot3D p;
int N = 64;
for (int i = 0; i < N; ++i) {
float y = float(i) / N;
for (int j = 0; j < N; ++j) {
float x = float(j) / N;
float value = f(x, y);
mpfr_float_1000 truth = f_truth(x, y);
float e = flulp_error<mpfr_float_1000>(value, truth);
p.add(x, y, e);
}
p.next_row();
}
p.show("log(x/y)", 0.0, 16.0);

なかなか誤差が大きいエリアがあることが見て取れます。どうやら が1に近いエリアでどうやら数値が暴れています。これは先に述べたlogのバッドランドそのものです。割り算の結果が丸められ、その誤差がバッドランドで伝播・拡大したことが原因と考えられます。バッドランドリストによれば、logのバッドランドは、
のエリアがバッドランドであり、このエリアだけ回避するのが良いと思われます。そこで、ここではlogを直接使うのではなく、以下の関数を活用することを考えます。
どうやらいろんな環境でも提供されている関数のようです。
std::log1p, std::log1pf, std::log1pl - cppreference.com
これのバッドランドは、オリジナルとは少しずれています。

ここで、これを使うように式を変形します。
このとき、 は、
であるとき、
となりますので、これが のバッドランドを踏んでいなければ良さそうです。確認してみます。

エクセレント!大丈夫のようです。これを試してみましょう。
float f_enhanced(float x, float y) { static const float lower = std::exp(-0.25f); static const float upper = std::exp(+0.25f); float x_div_y = x / y; if (lower <= x_div_y && x_div_y < upper) { return log1p((x - y) / y); } return log(x_div_y); }

2ulpを超える所がすべて排除されています!
ところでじゃあ最初から、
を使うのはダメなんだろうか?というのが頭をよぎります。試してみます。

確かにもともと存在していた山は改善しています。しかし、端の 付近では誤差が大きいことがわかります。
は x が0なら、 になるわけで、おっと、この場所はlogp1のバッドランドではありませんか!
というわけで結局今回のアプローチでは片方だけではうまくいかないということになります。
ちなみにこの話にはまだ続きがあり、Neil Toronto and Jay McCarthy | Brigham Young University, "Practically Accurate Floating-Point Math" にはさらにロバストにするには、という話もありますし、他の例もありますので、興味のある方は覗いてみると良いと思います。
まとめ
IEEE 754 浮動小数点の内部表現から、誤差の定式化、そしてどのような回避方法があるのかを調べ、そして簡単な改善アプローチを紹介しました。しかし実際に活用する時には、対処したい問題のドメインの知識もさらに加わりますし、6次元、7次元の関数を組み立てるときの対処方法についてもまだあまり良いアプローチを確立できていません。誤差の定式化も、これが最善かというと、確信は持てません。非正規化数のパフォーマンスの低下、フラッシュによる誤差の問題もあります。このように結局銀の弾丸はまだありませんが、浮動小数点がブラックボックスである状況に比べたら余程対策の立てようがあるのではないでしょうか。また、誤差を改善しました、という系の論文を読むときにもこの知識は大いに役に立つのではないかと思います。
参考文献
FLOATING POINT VISUALLY EXPLAINED
Neil Toronto and Jay McCarthy | Brigham Young University, "Practically Accurate Floating-Point Math"
GDC Vault - Math for Game Developers: Understanding and Tracing Numerical Errors in C++
Boost Interval Arithmetic Library - 1.70.0
Floating Point | Random ASCII – tech blog of Bruce Dawson

A Practical Microcylinder Appearance Model for Cloth Rendering to implementation (2)
The previous article is here.
日本語でも良い方はこちらを ( If you like Japanese, please check this )
Shading Model
Like the following figure, this paper makes shading model from warp and weft that is orthogonal.

It shows that each thread has different areas. So the following radiance formulation uses this fact.
where is simply parameters. If this is an interpolation, two a is unnecessary. But fig. 2 left picture shows there are cases that cloth contains some gap. In this case
. So we need two a. In contrast,
if cloth contains no gap.
Each is defined by
※ This is BRDF, so is a hemisphere.
Where is sample count of tangents because a thread is weaving at least one. We must evaluate each tangent contribution and the average is the final value.

※ Fig. 12, Polyester Satin Charmeuse fabric IMAN SADEGHI, OLEG BISKER, JOACHIM DE DEKEN, HENRIK WANN JENSEN, UC San Diego, "Practical Microcylinder Appearance Model for Cloth Rendering"
is previous thread model.
There was no reference for how to concretely sample in the paper. In this time I decided to use the control point at Table II in the paper as the sample point. Although this may not be good, I got an image that has a good match with the rendered image of the paper. I think it is a possible stochastic unbiased evaluation, but I think it is not clear whether the final result will lead to better results.
Although the whole flow can be covered above, in this paper, two more adjustments are presented to make it closer to the measurement result. This is "Shadowing and Masking" and "Reweighting".
Shadowing and Masking
Shadowing, masking function must be chosen suitable this shading model that is based on orthogonal warp and weft. So it is defined by
Where M depend on only . The reason is clear at Fig 13 in this paper.

※ Fig. 13, Center, Right Figure, Polyester Satin Charmeuse fabric IMAN SADEGHI, OLEG BISKER, JOACHIM DE DEKEN, HENRIK WANN JENSEN, UC San Diego, "Practical Microcylinder Appearance Model for Cloth Rendering"
In left-hand side, the thread isn't shadowed by other thread because the tilt direction is same to thread direction. But right-hand side, the thread can be shadowed by other thread. So, Shadowing, Masking use only angle.
Next, why we use in Shadowing, Masking ? This is because of a cylinder shadow. Please check following two cylinders in cylinder array. A white one cast a shadow on some of the gray one.

I'll show visibility in expression. These cylinder radius is 0.5.

So, visibility is .
Correlations of Shadowing, Masking
If Shadowing, Masking are assumed that has no correlations, Shadowing & Masking is defined by the following formulation using a simple product.
But this assumption has well-known problem at e.g. case. The visible area is exactly the same in this case, Masking both express surface visibility. Despite only on one side is enough to express the visibility, the product of the above formulation is overkill. This is a typical case that no-correlation assumption does not work well. Against this, a shadowing & masking combination method proposed at Michael Ashikhmin, Simon Premoze, Peter Shirley, "A Microfacet-based BRDF Generator" is chosen in this paper.
This idea is simple, we define the following expression as Shadowing & Masking function with strong correlation contrast to no correlation formulation.
I think "Shadowing area contains Masking area" or "Masking area contains Shadowing area".
Finally, we interpolate linearly to
by "similarity between incident direction and outgoing direction ".
Where "similarity between incident direction and outgoing direction" is a unit-height gaussian function that taking as its argument
Where is between 15 deg to 25 deg, I chose 20 deg for my implementation. However, it will not change so much when it is 15 degrees or 25 degrees.
And we can rewrite each shading model by
Reweighting
Let's start with fig 13 in this paper for thinking of Reweighting.

It looks the blue thread at the center is strong and its edge (=grazing angle) is weak blue. Because an apparent length( projected length to view direction ) of a thread is shorter by tilting it. Conversely, the orange thread apparent length looks uniform in any position.
So apparent length depends on only .
※ I have another idea that the blue thread weakness variation is caused by the orange thread apparent density. But the orange thread apparent density depends on the projected length of the blue thread to view direction. So, it is equivalent.
We can imagine this phenomenon like this.

It looks like "distribution of visible normal" in microfacet theory.
is not exist in my "Coordinate System" section. It is shown at Fig 14 in this paper.

It is a clear definition. The angle is in plane of thread direction and cloth normal.
A apparent length is expressed by . The new weight function is defined by
Coincidentally it is the same formula as Shadowing, Masking. Why considering not only outgoing direction but also incident direction is that there is the same phenomenon when light receives at a thread. The final contribution increases as apparent length are longer because it can receive more light. However, LTE contains that is considering of radiance density variation. So I think it is a little bit overkill. But it has a difference that
term depends on only
, so it may have different significance.
In the paper, because the idea is similar to Shadowing, Masking, the same definitions for incoming and outgoing is chosen.
Where is
. This is same idea to
.
We can rewrite the shading model with adding new weighting function.
There is normalize term . It is because that
cause energy scaling as A sum of
weight is not 1. It different from Shadowing, Masking.
is
It is a bit confusing. So I'll check each sample weight before adding Reweighting with the following figure.

The outside box has a unit area (= 1) in this figure. And it separated by parameters . Each thread has samples at least one, it is assigned a uniform weight in its thread. Where each weight is area assigned to sample.
We can regard that added into shading model scale the each area. So we must normalize by division by a sum of scaled area. The right term
support
case, it handle no-thread part using simply normal.
Implementation
My implantation is straightforward. I'll show this without embed by link because it is too long.
3d Model
I have prepared the shading model but It needs a 3d model for cloth. And I need to reproduce this paper rendering image, so I want to 3d model very close to the paper image. I heard Houdini 17 got new simulation module Vellum, so I'll try it.
※ Houdini17 have crashed sometime in My MSI laptop pc because of Nahimic. Houdini 17 crashing constantly - General Houdini Questions - od|forum And it has an initialization problem for OpenCL [Solved] OpenCL setup for 17? | Forums | SideFX. But this is maybe environment-dependent, so stop to talk about this problem.
Vellum is constraint-based solver highly inspired by Matthias Müller, Bruno Heidelberger, Marcus Hennix, John Ratcliff, "Position Based Dynamics". It is easy for example it can be completed only on "sop". So I'll introduce it.
Vellum
First, I make simple ground with Tube and Grid.

Next, I prepare cloth with appropriate density above the ground. it must be added uv by "uvflatten" for tangent vector calculation.

Next, I prepare constraint. There is cloth preset in houdini for a shortcut.

The stiffness at Bend can control difficulty in cloth bending. Since there are not so many parameters, if you don't like it, it is a good idea to modify the parameters. However, I heard from my friend who familiar with the simulation, "if it is possible, you should try experimenting with the cloth in hand" . There is a case you don't notice that approach is wrong with the only simulation.
We can check the constraint by connecting to null.

connecting to Vellum Solver for simulation.

We can tune friction with about "Forces/Friction/Static Threshold" parameters. If the constraints don't converge, I suggest increasing "Solver/Substeps".
Finally, Let's start the timeline.

it's easy!
I export obj at the appropriate frame by "File Cache" after "Smooth", "Subdivide" for adjustment.

The tangent vector can be prepared any method any timing but I precalculate it by "polyframe" in houdini.

※ This is vertex-based calculation. so I adjusted it the vector orthogonal in primitive.
That's all for preparation of 3d model.
Results
I used the following scene. (Actually, it arranged so as to approach the rendered image of the paper. )

These image by Table Ⅱ parameter in this paper.
Linen Plain

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.46 | Both | (0.2, 0.8, 1.0) * 0.3 | 0.3 | 12 | 24 | 0.33 | -25, 25 |
Silk Crepe de Chine

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.345 | Flat | (1.0, 0.95, 0.05) * 0.12 | 0.2 | 5 | 10 | 0.75 | -35, -35, 35, 35 |
| 1.345 | Twist | (1.0, 0.95, 0.05) * 0.16 | 0.3 | 18 | 32 | 0.25 | 0, 0 |
Polyester Satin Charmeuse

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.539 | Flat | (1.0, 0.37, 0.3) * 0.035 | 0.1 | 2.5 | 5 | 0.9 | -32, -32, -18, 0, 0 , 18, 32, 32 |
| 1.539 | Twist | (1.0, 0.37, 0.3) * 0.02 | 0.7 | 30 | 60 | 0.1 | 0, 0 |
Polyester Satin Charmeuse (Back-side)

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.539 | Flat | (1.0, 0.37, 0.3) * 0.035 | 0.1 | 2.5 | 5 | 0.67 | -30, -30, 30, 30, -5, -5, 5, 5 |
| 1.539 | Twist | (1.0, 0.37, 0.3) * 0.02 | 0.7 | 30 | 60 | 0.33 | 0, 0 |
Silk Shot

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.345 | Dir 1 | (0.1, 1.0, 0.4) * 0.2 | 0.1 | 4 | 8 | 0.86 | -25, -25, 25, 25 |
| 1.345 | Dir2 | (1.0, 0.0, 0.1) * 0.6 | 0.1 | 5 | 10 | 0.14 | 0, 0 |
Velvet
For some reason my Velvet did not match the result with the pictures of the papers. Perhaps it may be adjusting lighting and normals map to show the Siggraph logo.

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.46 | Dir 1 | (0.05, 0.02, 0.0) * 0.3 | 0.1 | 6 | 12 | 0.5 | -90, -50 |
| 1.46 | Dir2 | (0.05, 0.02, 0.0) * 0.3 | 0.1 | 6 | 12 | 0.5 | -90, -55, 55, 90 |
Fig. 24 in the paper

I could reproduce these render image except Velvet.
Impressions and Conclusion
I implemented velvet shading at ray tracing camp 6 . but I would try because I was short of the survey. The implementation of "A Practical Microcylinder Appearance Model for Cloth Rendering" looks not so heavy for me. However, the source code example could not be obtained, so it took quite some time.
This method might not be a sophisticated method, or it might be difficult to say Mathematically well defined. But this method is using minimum formulation for matching to measurement data, although it is only Far Field, I feel a pretty real taste. I think the point of view of this paper is so great.
「近似」は物理でとっても大事にゃ♡鉛筆では絶対に解けない(と証明されてる)積分や方程式も極端な状況や本質的な部分に着目してそれ以外を無視する「近似」を入れると解けたりして、そしてそれでオッケーって事も多いのっ 何を重要とみなすかはその時々、物理屋の実力が問われるにゃ>< →
— 物理学科に入学した凛ちゃんbot (@RinPhysBot) 2016年10月19日
She says...
"approximate" is very important in Physics ♡. An integral, equation that can't be solved (Proofed) exist but if these take "approximate" that ignoring some part excluding the extreme conditions or essentials component, it could be solved, and it's often no problem. What it is treated as important depends on the circumstance, so this is a good time to show their skills. ><
※ にゃ=meow, (her favorite way of talking)
On the other hand, energy conservation problems and the cost of shaders still have many tasks, and in particular, I think that it is difficult to intuitively prepare the parameters of Tangent Offsets. In addition, we easy to see details of the cloth, so far-field rendering is important.
Cloth shading technology has many compatibilities to hair and fur shading so we can see a wide range of knowledge on the way. If you are interested in this field, it would be interesting to look it up.
Acknowledgment
In implementing, Mr. Henrik W. Jensen has answered some questions by e-mail and helped me to understand well. Thank you so much.
References
※ You can see their presentation video if you purchase at ACM Digital Library
Iman Sadeghi, "Controlling the Appearance of Specular Microstructures"
Michael Ashikhmin, Simon Premoze, Peter Shirley, "A microfacet-based brdf generator"
Piti Irawan, "Appearance of Woven Cloth"
Stephen R. Marschner, Henrik Wann Jensen, Mike Cammarano, "Light Scattering from Human Hair Fibers"
Subrahmanyan Chandrasekhar, "Radiative Transfer"
Michael Ashikhmin, Simon Premoze, Peter Shirley, "A Microfacet-based BRDF Generator"
Matthias Müller, Bruno Heidelberger, Marcus Hennix, John Ratcliff, "Position Based Dynamics"
A Practical Microcylinder Appearance Model for Cloth Rendering to Implementation (1)
This article is a day 22 part of raytracing advent calendar 2018
Sorry for late!
日本語でも良い方はこちらを ( If you like Japanese, please check this )
Cloth and Fiber
There are several categories fibers used in cloth. For example, animal, plant and synthetic. Let's check.
animal
| Name | Based on |
|---|---|
| Wool | Fur of sheep |
| Cashmere | Fur of cashmere goat |
| Silk | Silkworm cocoon |
| Mohair | Angora goat |
plant
| Name | Based on |
|---|---|
| Cotton | Cotton plants of the genus Gossypium in the mallow family Malvaceae |
| Linen | Linum |
| Ramie | Boehmeria nivea |
synthetic
| Name | Based on |
|---|---|
| Polyester | Petroleum etc. |
| Nylon | Coal or petroleum |
Each of these fibers is a one-dimensional structure. Clothes need to make two-dimensional plane by some structure. For example, Felt is a sheet of entangled wool. We classify such cloth as nonwoven fabric (Nonwoven fabric) .

※ Nonwoven fabric(zoom)不織布 - Wikipedia より
In contrast, a cloth by wave orthogonal thread, it is named "woven cloth".

※ Silk Crepe de Chine (zoom) IMAN SADEGHI, OLEG BISKER, JOACHIM DE DEKEN, HENRIK WANN JENSEN, UC San Diego, "Practical Microcylinder Appearance Model for Cloth Rendering"
Other than these, "knitting" is that created by make looping structure and connect vertically and horizontally with curved thread.

※ 信州大学繊維学部, はじめて学ぶ繊維 P.140
We use knitting cloth for T-shirt, socks and Sportswear because of elasticity from this structure.

※ 信州大学繊維学部, はじめて学ぶ繊維 P.140
Cloth shading model
Many people have researched cloth shading, for a long time. The old one is Michael Ashikhmin, Simon Premoze, Peter Shirley, "A microfacet-based brdf generator" , mention to microfacet based Satin, Velvet shading model. Irawan, Marschner proposed massive woven cloth BRDF(Piti Irawan, "Appearance of Woven Cloth"). This support large-scale and small-scale analytic shading model. It is implemented to Mitsuba render But...it is too difficult for me...
These models are a surface-based approach. But there are some volumetric approaches. Wenzel Jakob, Adam Arbree, Jonathan T. Moon, Kavita Bala, Steve Marschner, "radiative transfer framework for rendering, materials with anisotropic structure" , Its scarf image is amazing.

※ Figure 1 (a) Isotropic scattering. Wenzel Jakob, Adam Arbree, Jonathan T. Moon, Kavita Bala, Steve Marschner, "radiative transfer framework for rendering, materials with anisotropic structure"
There are many interesting papers, but I have chosen woven cloth shading model described at IMAN SADEGHI, OLEG BISKER, JOACHIM DE DEKEN, HENRIK WANN JENSEN, UC San Diego, "Practical Microcylinder Appearance Model for Cloth Rendering" . This model support only large-scale appearance, the appearance of individual threads is ignored. But it can reproduce cloth anisotropic behavior and It is a good match to measured cloth BRDF. Additionary, the rendered image is very impressive, in particular, Silk Shot Fabric.

This characteristic gradation is caused by weft and warp threads that have each different color.
A Practical Microcylinder Appearance Model for Cloth Rendering

This approach in this paper has the following flow.
- BSDF measurement for individual threads.
- Create a shading model for individual threads.
- Create a BRDF model by two orthogonal threads.
- Tuning the visibility and shading from a woven pattern and tangent distribution.
- Apply Shadowing and Masking, and tuning shading weight from its tangent ( in this paper, called "Reweighting").
Coordinate System
Let's check the coordinate system at Fig. 9 in the paper.

is an angle from the normal plane of thread t.
is an angle from cloth normal in thread normal plane.
But is not used for indivisual thread bsdf model. Instead of this,
An amount such as above is used for thread bsdf.
Let's check the significance of each angle.
is a difference angle between incident angle
and outgoing angle
.
is a middle angle between incident angle
and outgoing angle
. As this is closer to 0, the specular reflection component becomes stronger.
is half angle from difference angle between incident angle
and outgoing angle
. In other words,
it is angle between
and
.
※ is half angle but
is not half. This cause little bit confusing. But I use the same definition according to this paper.
Incidentally, Iman Sadeghi's Ph.D. Thesis "Controlling the Appearance of Specular Microstructures" use no half angle at "5.2 Background Theory".
Thread model
We will describe a thread bsdf model by using above the angle definition. A thread is assumed that it is a rough dielectric cylinder, it is defined by the following two functions.
Where is specular component on cylinder surface,
is volumetric scattering component in cylinder. What is the denominator
? So I will think about this.
denominator 
If cylinder surface is perfectly smooth, incident light is reflected angle. The fact is already mentioned at もふもふレンダリング(3) . But I visualize this behavior following.

So, we can define a scattering function by using δ function.
Where is density function,
Additionally, I'll check the energy conservation.
The term is works well. It is essential term for discribe something.
The angle θ can be anything angle, but is this scattering invariant? I'll check two extreme cases.
First, case.

Second, case.

First case rays is higher density than second case rays. As is closer to
,
becomes bigger and bigger, so
term expresses this change of density.
Extending from δ function
Stephen R. Marschner, Henrik Wann Jensen, Mike Cammarano, "Light Scattering from Human Hair Fibers" extend the above scattering models to a rough surface.
is no longer true. It use
instead of this, but it is approximate.
So thread bsdf model in the paper contains
term because of this.
Specular component 
Specular component is defined following equation.
Where is fresnel term and
is normalized gaussian function (average is zero). I'll discuss the fresnel term later,
is
is a middle angle between incident angle
and outgoing angle
. So as
close to 0, the specular component is more stronger. Also we can modify the lobe shape by changing the variance.

※I ignore fresnel term in this plot.
What is  ?
?
has a characteristic shape. This is

※ desmos : cos(theta/2)
This is based on a considering of distribution rays reflection from a smooth cylinder. I'll show this visualization by raytracing.

It shows that the reflected rays have a high density as incident angle close to an outgoing angle. Conversely, as an incident angle far from an outgoing angle, the reflected rays have low density. I will think about this property.

In this picture, we can see the relationship between and the point P.
Where a incident ray is reflected to as a outgoing ray.

So,
Using this fact, we get the following relationship and
.
The derivative is
Where is smallness x per smallness reflected angle. It shows how distrebutions the smallness x belonging to unit length (=1) has.
So, in the above section "Extending from δ function" , N can be
And, the integration in a around must be 1 because of N is density function.
We can use the following derivative
So,
We have verified. So specular component equation
come from here.
Missing 
But, there is no in this equation! Actually, In Eugene d’Eon, Guillaume Francois, Martin Hill, Joe Letteri, Jean-Marie Aubry, "An Energy-Conserving Hair Reflectance Model"
When,
Then,
Figure 3 shows how amount this expression value, as several , as changing
.

I have plotted graph to verify by using this implementation.
It shows

※ unit is degrees, the horizontal unit is an outgoing angle (unit: radians), the vertical unit is outgoing radiance.
※ Total reflectance from cylinders - Google スプレッドシート
This is exactly same to Eugene d’Eon, Guillaume Francois, Martin Hill, Joe Letteri, Jean-Marie Aubry, "An Energy-Conserving Hair Reflectance Model" Figure 3. So the energy amplifies in the most part of this. This fact causes a motivation to introduce energy conservation Mp function from spherical gaussian.
From this, specular component has potential amplify the energy 4 times from above expression.
But, it is not a mistake. IMAN SADEGHI, OLEG BISKER, JOACHIM DE DEKEN, HENRIK WANN JENSEN, UC San Diego, "Practical Microcylinder Appearance Model for Cloth Rendering" has no energy conservation description. It is not the focal point in this paper. So I'll finish this study, go next.
Fresnel Term
Fresnel term is defined by
Sorry...I can't find where is come from. But and
is both angle from half angle. And a product of these terms means that the angle is treated as grazing angle if either one of the cosine of them approaches 0. In this paper says "We considered using the full microfacet specular formulation, but found that it did not improve the matching to our measured results".
I choose the following fresnel expression as fresnel term from Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces". It describes as "A convenient exact formulation for dielectrics with unpolarized light".
Volume scattering component 
is defined by
Where A is a spectrum dependence absorption coefficient. The coefficient that the specular component doesn't contain makes outgoing light colored.
F Term
F is defined by following expression in this paper.
But I don't find more details in the paper, but maybe
and,
is undefined in the paper. However, If cylinder volume multiple scattering is assumed that is described by the term,
is not so bad, I think. but I choose the following expression for my implementation.
 Term
Term
effect is exactly same to specular component
without the variance parameter. So it is modeled that refracted rays has same behavior with reflected rays on cylinder surface (= these has same
). Is it ture ? Let's check this by tracking refracted rays into a smooth dielectric cylinder. ( Houdini vex: tracking refraction · GitHub )

Where the incident rays has = 45° . And plotting its
shows

Surprisingly, all of the outgoing vectors is exactly the same angle to its incident angle. It has the same behavior even if use other incident angles. This fact is already showed at Stephen R. Marschner, Henrik Wann Jensen, Mike Cammarano, "Light Scattering from Human Hair Fibers" , section "A Loci of reflections". This is the figure 16. In the explanation of "A Loci of reflections", this is explained by treating the normal of the dielectric cylinder as the normal of the equator of the sphere.

※ The part with n, n 'is the cylinder normal.
where on sphere is seen incident vector. And this incident vector
can intersect with various normals on the equator (only front-side,
). First, I'll talk about typical normal
directly under
.
The refract to
with a relative refractive index with surface normal
. With snell's law,
where , we get
What is ? Geometrically, we can treat that it is
in the figure respectively. So we get
But normal is not only on the figure but also it can be any vector on the equator of the sphere. Let's check the following figure for other cases
.

※ I add that
of
.
where a amount of projected to Y axis is
I consider what value it will be. First, with Snell's law,
So,
Next,
Because of the above equation, we get
Then, vector direction is exactly inverse of
direction . So,
Using this, we get
Oh, I remember .
It says that a vertical distance of refracted vector from equator plane depend on only refractive index for any . In addition, considering that it goes out after entering from the dielectric cylinder, the refractive indices cancel each other out, and when exiting it exits at the same θ as incident θ (although it will reverse about positive and negative).
Because of this, term in volume scattering component is plausible. Although it is modeled with a rough dielectric cylinder, it seems that the light that enters inside will repeat scattering inside it. So, g in the volume scattering component has a different variance parameter from the specular component. And all of
is greater than
on Table Ⅱin this paper.
Denominator 
In this paper says "The division by the sum of projected cosines comes from Chandrasekhar [1960], in his derivation for diffuse reflectance due to multiple scattering in a semi-infinite medium." I'm afraid I can't understand these details because of my limited knowledge. But the paper says that this term has an effect to match more to brdf measurements.
※ Chandrasekhar [1960] = Subrahmanyan Chandrasekhar, "Radiative Transfer"
 term
term
term simply express isotropic scattering for cotton, linen, and so on. It interpolate
to
.
I'll show specular component lobe. It's intuitive I think.

I have completed introducing modeling of an individual thread. Next I will describe the shading model by using this.
A Practical Microcylinder Appearance Model for Cloth Rendering の実装(2)
前回からの続きです。
If you like english version, Please check this
シェーディングモデル
本論文では、以下の図のように2本のたて糸とよこ糸が図のように直行している様子をモデル化します。

図を見て分かる通り、明らかに たて(経)糸とよこ(緯)糸で見えている面積が異なります。これをシンプルに反映し、以下の式で出射放射輝度を定義します。
ここで、 は単純にパラメーターです。線形補間なら、aは一つでいいのではないか?とも思われるのですが、Fig. 2の一番左のように隙間が存在しているケースでは、
は必ずしも 1になりません。そのためこのパラメーターは2つ存在しています。逆に密に糸が織られているケースでは、
になります。
では個別の ですが、こちらは以下のように定義します。
※ もうBRDFを考えており、ここで は半球です。
ここで は何かというと、接線のサンプル数になります。というのも、織布の糸を考えたとき、少なくともどちらか1本は波打っていると考えられるため、その糸の傾き具合をそれぞれ別に評価して平均する、ということになります。

※ Fig. 12, Polyester Satin Charmeuse fabric IMAN SADEGHI, OLEG BISKER, JOACHIM DE DEKEN, HENRIK WANN JENSEN, UC San Diego, "Practical Microcylinder Appearance Model for Cloth Rendering"
については、前回の糸モデルそのままです。
サンプルを具体的にどうするのかは、論文には言及がありませんでした。今回は横着して、論文にある Table II の制御点をそのままサンプルポイントとすることにしました。これでも論文の画像と良好な一致を確認しました。しかし厳密には確率的に解いたりすると良いのかもしれませんが、最終結果により良い結果につながるかは疑問です。
以上で全体の流れは網羅できましたが、本論文ではより測定結果に近づけるため、さらに2つの調整を提示しています。それは "Shadowing and Masking"と"Reweighting" です。これについて見ていきます。
Shadowing and Masking
たて糸とよこ糸が直行している今回のようなシェーディングにマッチするShadowing, Maskingとして、 本論文では、それぞれ以下のように定義されています。
これを見てすぐに分かることとして、それぞれ にのみ依存する点があります。これの理由は、論文のFig 13がわかりやすいです。

※ Fig. 13, 中, 右の図 Polyester Satin Charmeuse fabric IMAN SADEGHI, OLEG BISKER, JOACHIM DE DEKEN, HENRIK WANN JENSEN, UC San Diego, "Practical Microcylinder Appearance Model for Cloth Rendering"
左の図を見ると、グレージング角でも糸が糸に隠れているところは存在しません。これは糸の方向と同一方向に傾いているからですね。 ところが右の図では糸の方向に対して横方向に傾いています。この場合は隣の糸に邪魔されて糸が隠れています。すなわちこの方向にのみShadowing, Maskingを考慮すれば良いだろう、ということになります。
では次になぜShadowing, Maskingは なのでしょうか。
これはシリンダーが横に並んだときの遮蔽を考えています。以下のようにシリンダーが横に並ぶと、手前の白のシリンダーが奥のグレーのシリンダーの一部を遮蔽します。

ではその見えている量はどのくらいかを、図に書き込んでみます。円筒の半径は0.5だとします。

そう、見えている量はまさに であったのです。
Shadowing, Masking の相関
もし入射と出射のShadowing, Maskingに全く相関が無い(=無相関)と仮定すると、Shadowing & Masking関数は以下のような個別の関数の単純な積の定義が用いられます。
しかしこの仮定にはよく知られた問題があって、例えば のようなケースを考えてみます。Shadowing, Maskingはどちらも表面の遮蔽具合を表現するものであるため、入射と出射が等しいのであれば、その見えている領域は完全に同一であるはずです。つまり、遮蔽に関して言えば実際には片方だけ作用させれば良いはずなのにもかかわらず、上記の定義ではそれの積、つまり二乗分の遮蔽が計上されてしまうのです。これは相関の仮定がうまく動作しないわかりやすい例です。
本論文ではこれの対策として、Michael Ashikhmin, Simon Premoze, Peter Shirley, "A Microfacet-based BRDF Generator" で提案されている方法を使っています。
このアイディアはシンプルで、入射と出射が等しいような強い相関のあるShadowing & Masking関数を、無相関とは対照的に、
と定義します。これは直観的にはShadowingの領域がMaskingの領域を包含している、もしくはMaskingの領域がShadowingの領域を包含していたので、遮蔽は大きい方に合わせれば良い、というイメージだと思います。
最後に無相関の関数と、強い相関のある関数を、"入射と出射の類似度" で線形補間します。
ここで、"入射と出射の類似度" は、 と
の差である、
を引数に取るガウス関数を用いて、
を使います。 については、15度から 25度となっていたため、ここではひとまず 20度で実装しました。ただ、15度や25度になったところでそれほど大きくは変わらないでしょう。
これにより、個別のシェーディングモデルは以下のように書き直されます。
Reweighting
Reweightingは、まず論文 Fig 13 を見てみましょう。

まず青色の糸に着目してみると、どうにも真ん中は青色が強く、端に行く(=グレージングアングルに近づく)ほどに相対的に青が弱くなっているのがわかります。
これは何故かと考えてみると、糸が傾くことで見かけの長さ(=視点方向へ投影した長さ)が小さくなっているからではないでしょうか。(=視点方向へ投影した長さ)が小さくなっているからではないでしょうか。
さらにオレンジの糸に着目してみると、全範囲で変化はなく均一です。これは端でもオレンジの糸の見かけ上の長さが変わっていないからでしょう。
このことから見かけ上の長さの変化は、 にのみ依存するということもわかります。
※ところで別な見方をすると、青色が弱く見えるのはオレンジの糸の密度が上がったからではないか?という考えも浮かびます。しかしオレンジの糸の密度が上がったのは見かけ上の青の糸が短くなったことに起因するわけで、結局同じことを違う視点で見ただけのようです。
イメージとしては以下のようなかんじでしょうか。

さながら、マイクロファセット理論でよく出てくる可視法線分布のようです。
は最初の座標系の説明には登場しませんでした。これも合わせて確認します。論文のFig. 14を確認しましょう。

わかりにくいところはなく、単に糸と同一方向と、布法線が作り出す面上の角度です。
では見かけ上の長さといえば、当然 です。論文ではこれを使って、以下の重みを定義しています。
偶然にも Shadowing, Masking と同一の式になっています。ちなみに入射と出射両方向考えているのは、見る方向だけでなく、光を受ける方も同様の現象がおこり、見かけ上の長さ長いほうが受光量が大きくなり、結果寄与がおおきくなるだろう、という考えがあるからです。しかしながら、入射のほうについては、LTEの放射輝度の密度変化を考慮した 項があるわけなので、両方向考えるのはいささか過剰な気もしますが、
にのみ依存する
項とは少し立ち位置が違うのかもしれません。
論文ではShadowing, Maskingとアイディアも似通っているからか、入射と出射の組み合わせについても、同様の以下の定義を用いています。
ここで、 は、
となります。
と同様の考え方ですね。
以上を重みを式に付け加えて以下のようにシェーディングモデルを書き直します。
正規化項として が増えています。今回追加した
項は重みを調整するための恣意的なスケールを行うわけですので、それ単体では重みの和が1にならず、エネルギー全体にスケールを掛けてしまう恐れがあるためです。ここはShadowing, Maskingと違うところですね。
は以下のように求めます。
ちょっとややこしいことになっています。 ここでReweightingを加える前では、全体から見ると個別のサンプルはどういう重みになっていたか?を図にしてみます。

この図では外側の箱がちょうど単位面積になっており、まずパラメーター によって二分されます。その後、それぞれの糸ごとに一つ以上のサンプルが存在し、それぞれ均一な重みが割り振られます。こう考えると個別のサンプルの重みは割り当てられた面積ということになります。
ということは結局のところ今回追加する は、この個別の面積をそれぞれスケールした と考えられます。スケール後の面積の和は1になりませんので、結局スケール後の面積の和で除算して正規化すれば良いことがわかります。
ちなみに最後の項
は
のケースを考慮しており、糸が存在していない部分はとりあえず法線に合わせた投影領域に重みを割り振ったと考え、残りを埋めています。
実装
実装は素直にストレートフォアードにやったつもりです。結構長いので埋め込まずリンクにしています。
モデル
シェーディングモデルは用意できましたが、絵を出すにはやはりモデルが必要で、また論文の絵をなるべく再現したかったので、それに近い3Dモデルがほしいです。ちょうどHoudini 17には新しいシミュレーションモジュール、Vellum が入ったそうなので、それを試してみることにしました。
※自分のMSI ノートでは、NahimicのせいでHoudini17がクラッシュしたり、Houdini 17 crashing constantly - General Houdini Questions - od|forum 、OpenCL の初期化でエラーでて設定を調整したりなどちょっと問題もありましたが・・・[Solved] OpenCL setup for 17? | Forums | SideFX 環境依存っぽかったのでこれについてはあまりここでは深入りしないことにします。
VellumはMatthias Müller, Bruno Heidelberger, Marcus Hennix, John Ratcliff, "Position Based Dynamics" をベースとしたソルバーのようで、拘束ベースで設定を行います。またSopで完結できるようになっていたりとかなり楽に使えてとても良かったので、ついでに紹介してみます。
Vellum
まずは地面を作ります。TubeとGridをただ並べるだけにします。

次に上に重ねる布を適当な分解能で準備します。ただ後に接ベクトルを計算のため、uvflattenを使ってpointにuvを追加しておきます。

次にConstraintを設定します。Clothはプリセットがあるのでそれを選ぶと楽です。

BendのStiffnessを調整すると、布の曲がりにくさを調整可能です。パラメーターはそれほど多くはないので狙った見た目にならない場合はちょっといじってみると良いでしょう。ただ、シミュレーションに詳しい人に聞いてみると、可能な場合は、実際手元で布をいじってみてどういう形になるのか?を試してみたほうが良い というのを聞きました。シミュレーションだけしかやっていないと、シミュレーションは正しいが、アプローチが間違っている場合に気づかないこともあるそうです。
真ん中をnullにつなぐと、拘束を確認することもできます。

心臓部、Vellum Solverにつなぎます。

Forces/Friction/Static Threshold などを調整して摩擦の具合を調整できます。 また、拘束が伸びすぎて収束していないようなケースでは、Solver/Substeps などを上げると良いでしょう。
あとはタイムラインをスタートすれば、

ね?簡単でしょう?
あとは適当なフレームで、Smoothと、Subdivideをかけてちょっと綺麗にしつつ File Cacheを使ってobj書き出しを行います。

接ベクトルは実行時に計算しても良いのかもしれませんが、今回はHoudiniのpolyframeパッチを使って事前計算しました。

※ただ頂点単位の計算になるので、実際には最後にプリミティブで接ベクトルがそれぞれ直交するように調整しています。
以上でモデルは準備完了です。
結果
シーンは以下のようにしました。(いや、正確には論文の絵に近づくように配置してみたところこうなりました、というのが実情です)

ここでは論文のTable Ⅱにあるパラメーターを使って再現してみます。
Linen Plain

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.46 | Both | (0.2, 0.8, 1.0) * 0.3 | 0.3 | 12 | 24 | 0.33 | -25, 25 |
Silk Crepe de Chine

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.345 | Flat | (1.0, 0.95, 0.05) * 0.12 | 0.2 | 5 | 10 | 0.75 | -35, -35, 35, 35 |
| 1.345 | Twist | (1.0, 0.95, 0.05) * 0.16 | 0.3 | 18 | 32 | 0.25 | 0, 0 |
Polyester Satin Charmeuse

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.539 | Flat | (1.0, 0.37, 0.3) * 0.035 | 0.1 | 2.5 | 5 | 0.9 | -32, -32, -18, 0, 0 , 18, 32, 32 |
| 1.539 | Twist | (1.0, 0.37, 0.3) * 0.02 | 0.7 | 30 | 60 | 0.1 | 0, 0 |
Polyester Satin Charmeuse (Back-side)

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.539 | Flat | (1.0, 0.37, 0.3) * 0.035 | 0.1 | 2.5 | 5 | 0.67 | -30, -30, 30, 30, -5, -5, 5, 5 |
| 1.539 | Twist | (1.0, 0.37, 0.3) * 0.02 | 0.7 | 30 | 60 | 0.33 | 0, 0 |
Silk Shot

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.345 | Dir 1 | (0.1, 1.0, 0.4) * 0.2 | 0.1 | 4 | 8 | 0.86 | -25, -25, 25, 25 |
| 1.345 | Dir2 | (1.0, 0.0, 0.1) * 0.6 | 0.1 | 5 | 10 | 0.14 | 0, 0 |
Velvet
なぜかVelvetに関しては結果が論文の写真とあまり合いませんでした もしかすると論文のはSiggraph ロゴを出すためにライティングや法線マップを調整しているのかもしれません。

| |
Thread | A | |
|
|
|
Tangent Offsets (deg) |
|---|---|---|---|---|---|---|---|
| 1.46 | Dir 1 | (0.05, 0.02, 0.0) * 0.3 | 0.1 | 6 | 12 | 0.5 | -90, -50 |
| 1.46 | Dir2 | (0.05, 0.02, 0.0) * 0.3 | 0.1 | 6 | 12 | 0.5 | -90, -55, 55, 90 |
論文 Fig. 24

Velvet以外については、無事再現することができました。
まとめ
レイトレ合宿6 ではベルベットのシェーディングをまがいなりにも導入していましたが、布のシェーディングについては正直ほとんど調べられておらず、やや不完全燃焼な印象があったので、一度ちゃんと調べてみたかったのもあり、ざっと調べた範囲で手の届きそうなところの A Practical Microcylinder Appearance Model for Cloth Renderingにチャレンジしてみました。ところがソースコードが入手できなかったのもあり、なかなか時間がかかってしまいました。
本手法は、決して洗練された方法でもないかもしれませんし、Mathematically well defined とも言いにくいかもしれません。しかし測定データに対して最小限の定式化を使い、Far Fieldだけとはいえ、かなり真実の味を感じる絵を実現しています。 何を重要とみなすか?というフォーカスの設定がここで肝だったのではないでしょうか。
「近似」は物理でとっても大事にゃ♡鉛筆では絶対に解けない(と証明されてる)積分や方程式も極端な状況や本質的な部分に着目してそれ以外を無視する「近似」を入れると解けたりして、そしてそれでオッケーって事も多いのっ 何を重要とみなすかはその時々、物理屋の実力が問われるにゃ>< →
— 物理学科に入学した凛ちゃんbot (@RinPhysBot) 2016年10月19日
一方で、エネルギー保存の問題や、シェーダの重さはまだ課題が多いですし、特にTangent Offsetsのパラメーターは直観的に設定するのは難しいと言わざるを得ません。また、布ではカメラが布にある程度近づくだけで詳細が見えてしまう実情もあり、さらなるクオリティアップのためには、Near Fieldの見た目をうまいことハンドリングするのは避けて通れない気もします。
布特性上、かなり毛髪などのレンダリングと理論が共通しているため、わりと幅広く知識がつながっている感触も得られました。ぜひこの分野に興味が湧いた方は調べてみると面白いのではないでしょうか。
謝辞
実装にあたって、Henrik W. Jensen 氏には、メールでいくつか質問に答えていただき、大きく理解を助けていただきました。本当にありがとうございました。
In implementing, Mr. Henrik W. Jensen have answered some questions by e-mail and helped me to understand well. Thank you so much.
参考文献
※ちなみに ACM Digital Library で課金すると、彼らのプレゼン映像が見れます。
Iman Sadeghi, "Controlling the Appearance of Specular Microstructures"
Michael Ashikhmin, Simon Premoze, Peter Shirley, "A microfacet-based brdf generator"
Piti Irawan, "Appearance of Woven Cloth"
Stephen R. Marschner, Henrik Wann Jensen, Mike Cammarano, "Light Scattering from Human Hair Fibers"
Subrahmanyan Chandrasekhar, "Radiative Transfer"
Michael Ashikhmin, Simon Premoze, Peter Shirley, "A Microfacet-based BRDF Generator"
Matthias Müller, Bruno Heidelberger, Marcus Hennix, John Ratcliff, "Position Based Dynamics"
A Practical Microcylinder Appearance Model for Cloth Rendering の実装(1)
この記事は レイトレアドベントカレンダー2018 22日目の記事です。
大遅刻しましてすみません!!!
If you like english version, Please check this
布と繊維
布に加工される繊維は多岐にわたりますが、大きな分類としてな、動物繊維・植物繊維・化学繊維といったものが存在し、 例えば以下のようなものがあります。
動物繊維
| 名前 | 原料 |
|---|---|
| 羊毛(Wool) | 羊の毛 |
| カシミヤ(Cashmere) | カシミヤ山羊の毛 |
| 絹(Silk) | 蚕の繭 |
| モヘア(Mohair) | アンゴラ山羊の毛 |
植物繊維
| 名前 | 原料 |
|---|---|
| 綿(Cotton) | ワタ(アオイ科ワタ属)の木綿(もめん) |
| リネン(Linen) | 亜麻 |
| ラミー(Ramie) | 苧麻 |
化学繊維
| 名前 | 原料 |
|---|---|
| ポリエステル(Polyester) | 石油等 |
| ナイロン(Nylon) | 石炭または石油 |
これら繊維はどれも1次元的な糸の状態です。布は、これらをなんらかの構造で平面の結合状態を作る必要があります。 例えばフェルトは、羊毛などを絡めてシート状にしたものです。このような布を 不織布(ふしょくふ, Nonwoven fabric) と分類します。

※ 不織布(拡大図)不織布 - Wikipedia より
これとは対照的に、直交する糸を上下させて作る布を 織布(woven cloth) と呼びます。

※ Silk Crepe de Chine の拡大写真 IMAN SADEGHI, OLEG BISKER, JOACHIM DE DEKEN, HENRIK WANN JENSEN, UC San Diego, "Practical Microcylinder Appearance Model for Cloth Rendering" より
これら以外では、 編物 または ニット(knit) とも呼ばれるものは、糸を屈曲させてループを作って前後左右に繋いだものを言います。

※ 信州大学繊維学部, はじめて学ぶ繊維 P.140
この構造から、伸縮性が得られるため、Tシャツや靴下やスポーツウェアにも使われます。

※ 信州大学繊維学部, はじめて学ぶ繊維 P.140
布のシェーディングモデル
布シェーディングについては古くより研究が多くなされています。古いものとしては、Michael Ashikhmin, Simon Premoze, Peter Shirley, "A microfacet-based brdf generator" ではマイクロファセットベースのサテン・ベルベットのモデル化にも触れられています。 大きなものとしては、Irawan, Marschner らが開発したwoven cloth BRDFのモデル(Piti Irawan, "Appearance of Woven Cloth")があり、こちらはラージスケールとスモールスケールをサポートする解析モデルで、Mitsuba にも実装されているそうです。しかしながら大規模すぎてちょっと自分には攻略できませんでした。
これらはサーフェイスベースのアプローチですが、ボリューメトリックなアプローチもあり、Wenzel Jakob, Adam Arbree, Jonathan T. Moon, Kavita Bala, Steve Marschner, "radiative transfer framework for rendering, materials with anisotropic structure" でのscarfの絵はとても美しく心惹かれるものがあります。

※ Figure 1 (a) Isotropic scattering. Wenzel Jakob, Adam Arbree, Jonathan T. Moon, Kavita Bala, Steve Marschner, "radiative transfer framework for rendering, materials with anisotropic structure" より
いろいろ目移りしますが、自分はボリュームレンダリングには不慣れなので、今回は織布のレンダリングにフォーカスした論文、IMAN SADEGHI, OLEG BISKER, JOACHIM DE DEKEN, HENRIK WANN JENSEN, UC San Diego, "Practical Microcylinder Appearance Model for Cloth Rendering" に着目します。これは織布にフォーカスしたもので、スモールスケールの糸の構造など無視されているものの、布の異方性反射をよく表現でき、計測したBRDFとよく適合するとあります。絵もなかなか綺麗で、Silk Shot Fabricは印象的です。

これはたて(経)糸とよこ(緯)糸に違う色が使われているからで、このモデルの特徴がよく表われていると言えます。
A Practical Microcylinder Appearance Model for Cloth Rendering

この論文のアプローチは、以下のような流れになっています。
- 布を構成する1本の糸についてのBSDF測定を行う
- 個別の糸をうまく表現できるモデルを用意して、パラメーターを調整
- 糸を垂直に2本並べたBRDFモデルを作る
- 織布の織りパターンに応じて可視性や、糸の角度分布ごとにシェーディングを行う
- Shadowing and Masking、および角度分布によるエネルギー再分布(論文ではReweighting)を考慮して重みを調整する
だいたいこんな感じです。
座標系
モデルに先立ってまずは座標系を確認します。論文中 Fig. 9 がわかりやすいです。

はスレッド t の 法線面からの角度
は 布文脈での法線からの、法線面における角度でありますが、糸単体では法線は面を形成することには注意が必要です
ただ図にある は、個別の糸BSDFモデルでは直接は使われません。代わりに、
といった量が使われます。
それぞれ意味を確認しておきます。
はそれぞれの入射
と出射
の差です。
は、入射
と出射
の中間の角度です。これが0に近いほど、鏡面反射成分が強くなることが想像できます。
はそれぞれの入射
と出射
の差の半分、言い換えると
と
の角度とも言えます。
※ は半分にされていないのに
が半分にされているのは、少し混乱しますね。でも論文の表記がそうなのでそれに揃えます。ちなみに Iman Sadeghi氏のPh.D. Thesis、"Controlling the Appearance of Specular Microstructures" では、5.2 Background Theoryでは両方とも半分になっておらず、統一されています。
糸のモデル
これらを使って、糸のモデルを記述します。糸は、誘導体のラフな円筒であると仮定されており、 糸のモデルは以下のように2つの関数で記述します。
ここで は円筒表面で反射する鏡面反射成分、
は円筒内部に入って出てくるボリューム拡散成分になります。では分母にある
は何か?これを少し考えてみます。
分母の 
仮に円筒表面が理想的になめらかであり、完全な鏡面であったとします。すると鏡面反射する光は、 の角度に対して
の角度に鏡面反射します。これは もふもふレンダリング(3)のMpの説明の一部 でも軽く紹介していました。改めてビジュアライズすると、

このことを踏まえて、拡散関数を以下のようにδ関数を使ってモデリングできます。
ここで、 を
の密度関数、
とします。
エネルギー保存について考えてみます。
ここでの係数 はうまく機能しています。この項は必要な係数であるのは明らかで、確かに何かを説明しているようです。
ところで角度θは様々な角度をとりますが、拡散の具合はそれぞれで果たして同じだろうか?というのを考えてみますと、例えば極端な2つのケースを考えて見ます。
まずは のケース

次に のケース

明らかに前者は後者に比べて、明らかに光線の密度が高いです。 が
に近づくと、
はどんどん大きくなっていきますので、つまりこの
項はこのことを説明していたのではないでしょうか。
δ関数からの拡張
Stephen R. Marschner, Henrik Wann Jensen, Mike Cammarano, "Light Scattering from Human Hair Fibers" では、以上のアイディアをもとにδ関数をラフな表面に拡張しています。それは、
というものです。 がもはや機能しないため、代わりに
が使われているのは、近似的ですが仕方のない側面があります。
そんなわけで、糸のモデルが
を含むのもこれを参考にしているからということになります。
鏡面反射成分 
鏡面反射成分は、以下のような式で表されます。
ここで はフレネル項、
は正規化ガウス関数で、平均は0です。フレネルは後ほど議論するとして、正規化ガウス関数は、
であり、 は、入射
と出射
の中間の角度であり、これが0に近づくと鏡面反射成分が強くなることを表現しています。また、分散を調整することでローブの形を調整できるようになっています。

※プロットではフレネル項は除いています
 はどこから来るのか?
はどこから来るのか?
次に、 の項は特徴的です。プロットしてみると、以下のようになります。

※ desmos : cos(theta/2)
これは、完全になめらかな円筒に入射した光線の反射が周囲にどのように分布するのかを考えたものになります。これについて実際に光線を飛ばして可視化してみますと、次のようになります。

入射と出射が近いところの密度は高く、離れるほど密度が小さくなっています。 ではこの密度の関係性は実際にはどうなっているか考えてみます。

まず図のように と点Pのxとの関係を考えて、これは当然、
となります。ここで、 の箇所に入射してきた光は、
のところに出射します。

したがって、
つまり、 と
には以下のような関係性があります。
これを微分して、
ここで とは何かと言えば、微小な反射角度あたりの微小なx、元は単位長さ(=1)の部分が反射角にどのように分配されるかを示しています。
つまり先の節 "δ関数からの拡張" のところのNの一つの形としては、
を使うことができることも意味します。 実際、密度関数なら、1回転分の積分が1になるはずで、
は、
から、
と検算で確かめることもできました。 というわけで、鏡面反射成分の式、
の はここから来ている、ということがわかりました。
消えた 
ところが、この式には がどこにもありません!
実際、Eugene d’Eon, Guillaume Francois, Martin Hill, Joe Letteri, Jean-Marie Aubry, "An Energy-Conserving Hair Reflectance Model" には、
のとき、
がいくつかの で、
を変えながら観察したとき、どうなるのか?という検証がFigure 3にのっています。

今回は、自分でも検証のために以下の実装でプロットしてみました。
これをグラフにすると、

※ の単位は度で、横軸は出射角度(ラジアン)、縦軸は出射放射輝度
※ Total reflectance from cylinders - Google スプレッドシート
これは確かに Eugene d’Eon, Guillaume Francois, Martin Hill, Joe Letteri, Jean-Marie Aubry, "An Energy-Conserving Hair Reflectance Model" の図と一致しており、かなり部分でエネルギーが増幅しているのがわかります。 そしてこれが球面ガウス関数を加工して作る "4.2. An Energy-Conserving Longitudinal Scattering Function Mp" の導入の大きな動機になっています。
つまりここから考えると、本論文の鏡面反射成分 はこれの結果のさらに4倍ものエネルギーを増やすポテンシャルがあることになります。
しかしながらこの部分が間違った記述というわけではどうやらなく、こういうもののようです。IMAN SADEGHI, OLEG BISKER, JOACHIM DE DEKEN, HENRIK WANN JENSEN, UC San Diego, "Practical Microcylinder Appearance Model for Cloth Rendering" にはそもそもエネルギー保存に関する記述は無く、この論文の興味の対象では無いのでしょう。ここでも考察はこのくらいにして、次に進みます。
フレネル項
フレネル項は、以下のように定義されています。
この項がどこから来たのか、ちょっとわかりませんでした。しかし、 も
も、ハーフアングルまでの角度であり、そのコサインの積ということは、どちらか一方でも0に近づけば、グレージング角で入射したことにする、というような意図は感じます。論文にはマイクロファセットを考慮したフレネル項の導入を検討したが、測定したデータとのマッチングに改善が見られなかった、とありました。
論文には記載がありませんでしたが、今回は誘導体フレネル項の計算には、Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces" の中で、"A convenient exact formulation for dielectrics with unpolarized light" として書かれている以下のものを使うことにしました。
ボリューム拡散成分 
続いて です。こちらは以下のように定義されています。
ここでAは波長依存の吸収係数、ここで色がつきます。この項は鏡面反射成分にはありませんでした。
F 項
Fはフレネル項で論文中では、
となっています。しかしこれ以上の言及はなかったのですが、おそらく、
であろうと思いつつ、
の項は意図がわかりません。とはいえ、シリンダー内部の多重拡散もこの で説明できると仮定すると、
としてしまうのもそれほど間違っているとは思えませんが、今回は、
で実装してみることにしました。
 項
項
次に、、この項は分散のパラメータが違うだけで、鏡面反射成分の中にある
と全く同じ働きをします。つまり反射成分だけでなく、一度屈折した光線も出るときにも
に関しては同じふるまいだとモデル化されています。これは真なのでしょうか? これを観察するために、なめらかな誘導体シリンダーへ入射する光線の屈折を追跡してみます。(Houdini vex: tracking refraction · GitHub )

ここで入射光線は = 45° であり、光線の
をプロットしてみると、

なんと、すべての出射ベクトルは、入射と全く同じ角度で出射しています。ちなみにこれは入射角度を変えても同様のふるまいをします。 実はこのことはすでに、Stephen R. Marschner, Henrik Wann Jensen, Mike Cammarano, "Light Scattering from Human Hair Fibers" の "A Loci of reflections" で触れられています。 "A Loci of reflections" の説明では、誘導体シリンダーの法線を、球体の赤道部分の法線と捉えることでこれを説明しています。

※ n, n'がある部分がシリンダー法線です。
ここで、球面上の点 を入射ベクトルと考えます。とするとこの入射ベクトル
は、赤道上のいろいろな法線と衝突する可能性があります(裏面、つまり
と
が反対向きでないケースに限りますが)。ここではまず代表的な法線、
の真下にある法線を
と表記します。
この と
の 組み合わせで屈折の振る舞いを考えて、ある相対屈折率では、屈折後は図の
のベクトルになりました。スネルの法則によれば、
の関係性があり、ここで、 とすると、
ここで は何か?と考えてみると、幾何学的にはそれぞれ図の
だと捉えることができます。
つまり、
という関係性を考える事ができます。
しかし法線は実際には だけでなく、赤道の上のどんなベクトルにもなりえます。そこで真下の法線ではない法線
について考えてみます。下の図をご覧ください。ここでは、
のケースの
にあたる部分、
を足しています。

このとき、 を Y 軸に投射した量、
はどんな値になるのか考えてみます。 まず、やはりスネルの法則によれば、
であるので、
次に、
であることから、
このとき、ベクトル と ベクトル
は、向きがちょうど正反対になります。したがって、
でなければばならないでしょう。これを使うと、
おっと、 であったことを思い出すと、
これの意味するところは、どのような であっても、屈折後のベクトルの赤道面からの垂直距離は屈折率にのみ支配されるということになります。加えて、誘導体シリンダーから入った後に出ることを考えると、屈折率は打ち消し合い、出るときには入るときの
と同じ
で出射する ということもまた言えることになります(正負については反転しますが)。
したがって、ボリューム拡散成分の 項はこの意味で妥当だと考えることができるでしょう。ただし、ラフな誘導体円筒でモデル化しているとはいえ、内部に入り込んだ光は中で拡散を繰り返すことが考えられ、今回のモデルでは、ボリューム拡散成分のgの分散は、鏡面反射とは違う分散を与えられるようになっており、元論文Table Ⅱに記載されているパラメーターも、すべて
は
よりも大きな分散を与えるようになっています。
分母の 
論文では、半無限媒質の多重散乱による拡散反射を考えたもの(Subrahmanyan Chandrasekhar, "Radiative Transfer")だとありますが、すみませんこの項についてはよくわかりませんでした。ただ、この項により測定値とよりマッチするようになったとのことです。
 項
項
項 はかなりシンプルで、綿やリネンなどの等方的な拡散を表すために、
と
を
で線形補間しています。
以上をプロットしてみると以下のようになります。以上の理解からすると、おおむね直観的な動きだと言えます。

これで個別の糸のモデル化が完了しました。次回はこれを使ってシェーディングモデルを構築します。
Stratified Sampling of Spherical Trianglesを読む
Stratified Sampling of Spherical Triangles
元論文は、James Arvo, "Stratified Sampling of Spherical Triangles" で、前回のこちらの関連になります。
James Arvo, "Stratified Sampling of Spherical Triangles" は、Spherical Rectanglesよりもだいぶ前の論文で、SIGGRAPH '95 の論文とのことです。Carlos Ureña, Marcos Fajardo, Alan King , “An Area-Preserving Parametrization for Spherical Rectangles” からも当然引用があります。
こちらもやはりモチベーションや達成したい目的は同じで、単位面積 から、任意の 三角形 の領域を単位球面に射影してできた領域への写像を、面積を保存する形で提示します。
球面三角法
やはりこの論文でも、球面三角形の性質をうまく使っていきます。 まずは前回も登場した、単位球面三角形の面積と頂点の角度の関係式、

そして、もう一つ単位球面三角形の角度の余弦定理と呼ばれる式、

※a, b, cは球面上の線の弧の長さです
が論文中の(1) ~ (3)にあります。
(1) については、前回触れていたので省略します。
また、導出については、
の説明が大変わかりやすく、オススメです。
しかし、単位球面三角形の角度の余弦定理についてはなんぞこれ?という感じがします。
イマイチイメージしずらいのですが、ちょっと特殊なケースについて試してみましょう。
例えば かつ
のケースです。この時は以下のようなシチュエーションになるでしょう。

赤い線を赤道だとすると、 の頂点はちょうど北極点(南極点)に位置します。
これは、先に
が決まっていたとして、
かつ
となるように線を引くとしたら以下のようにやはり真ん中を選ぶしか無いから、と考えると直観的です。

では式はどうなるかというと、
と
が直接結びつく形になりました。
これはある意味当たり前で、赤道の長さが
なので、
は、
となるからです。ちょっとだけ親近感が湧いてきました。このように単位球面三角形の角度の余弦定理は、ある1辺の長さと三角形の角度を繋げてくれるものだと言えます。 では一緒に導出のほうも見てみることにします。
これについては、張海潮 氏の、"球面三角形的AAA 定理" にわかりやすい解説があったのでこちらを見てみることにします。中国語ですが、google 翻訳があれば結構大丈夫です。
圖二(図2)の下を見てみます。

※張海潮, "球面三角形的AAA 定理" 圖二 より
記号については同じものを使っているので、混乱しなくて助かります。 はそれぞれ球の切り口の法線になります。
ここで2つのベクトル
と
を考えます。これはそれぞれ、球心からAに向かうべクトル、球心からCに向かうべクトルと向きが一致します。図にすると、

※長さは適当です
この時、さらにこの2つのベクトルの内積を考えます。
これは幸運にも スカラー4重積 の形をしており、
うまいこと球面三角形の角度だけで表すことができます。
他方、内積の定義、 から考えると、
ここでは∠AOCの角度であり、ということはつまり bの長さでもあります。
そして単位ベクトルの外積のベクトルの長さは
を使っても表せるので、これらを利用すると、
以上2つの式をつなげると、
となり、これが元論文の式 (2) に対応します。 論文には2つしか書かれていませんが、当然3つ式を考えることができます。
なかなか綺麗なものです。
The Sampling Algorithm
上記の式を使って、実際にサンプリングについて考えていきます。 本手法でも、前回と同じく2段階のアルゴリズムになっています。論文 Figure1を見てみましょう。

※James Arvo, "Stratified Sampling of Spherical Triangles" Figure 1 より
1段階目で 上の
を選択、2段階目で
上の
を選択する、といった具合です。
まずは1段階目から参ります。
ここでは球面三角形
に着目して、先程の球面三角形の角度の余弦定理のうち、
を決めるのに重要な量、
の両方が組み込まれている、
この式を出発点として考えてみます。
ここで、球面三角形 の面積を
、球面三角形
の面積を
とおくと、
※面積の記号として については、論文と違います。論文の記号がAとかぶってややこしいからです。
これを使うと、 をうまく置き換えることができ、
ここで一旦、 とおくと、
これが論文の式 (4)になります。
写像元の単位面積 の1つ目の変数を
とすると、
であることもついでに確認しておきます。
ここでポイントなのは、 が定まると、
が定まり、
が決まり、自動的に
が定まる、そうすれば
が定まりそうです。ただ論文の式 (4)にはまだ問題があって、
が残ってしまっています。本当はこの項は自動的に決まるはずであり、なんとか消したいと考えます。
ここで球面三角形 で球面三角形の角度の余弦定理をもう1パターン持ってきます。
これは論文の式(3)に対応します。この式に対して同様の操作をしてみます。
ここで加法定理でさらに続けて、
ここで一旦 に集中するため、以下のように、
とおくと、
とシンプルにまとめることができました。さらにここで、
の関係を使って、
ただ、符号については によって変えなければなりません。

そのことを一旦 と記述することにしますが、次に、
のように符号と逆になった項をかけます。すると、
結果的に最初の部分の符号については気にする必要はない状態で を得る事ができました。結局最後は符号が行方不明になってしまいましたが...。
についても同様の操作を行うと、
と、 についても、符号はともかく得ることができました。
さて、
をちょっとだけ変形してみると、
ここからわかることは、 と
は常に符号が逆にならなければならない、ということです。
それを踏まえて、
と
についても少しだけ変形してみると、
のようになります。
ここで、 が負のケースを考えてみると、両方とも右辺は常に正であることが求められますので、
逆に が負のケースは、
つまり結局のところ、
のように と
の符号はお互いに逆になるということになります。
※実際には
によって符号がフリップしますが、後の議論によってさほど本質的は問題ないことがわかります。
これを使って、少し戻ってしまいますが、論文の式(4)
にこれを代入していきます。
なんと、都合の良いことに、正負が打ち消し合って綺麗に消えてくれました。これが論文の式 (5) ということになります。最後の代入のおかげで、は完全に姿を消し、写像元の単位面積
の1つ目の変数
からダイレクトに
へと繋げる事ができました。
 を求める
を求める
が求まりましたので、次に実際にそこから
の値を求めていきます。
論文では記述の簡略化のために、以下の表記を使っています。
※ ここで yは単位ベクトルとします
これは、どういう演算かというと、
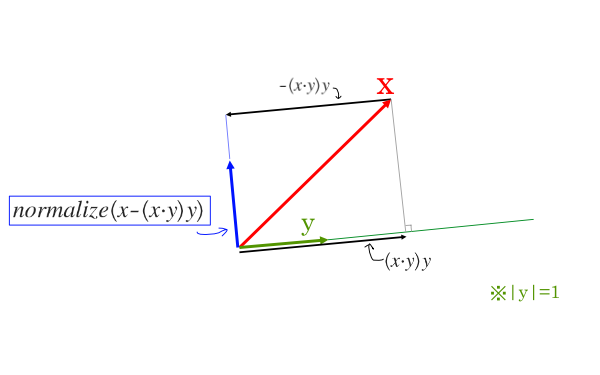
そう、x方向の、yと直交するベクトルを得る演算ということになります。 これを使えば、AからCに向かっての回転を簡単に考えることができます。

※もちろん、実装上クォータニオンなどを使って回転させるのも可能だと思いますが、こちらのやり方のほうがシンプルなように思いました。
また、今手元には しかありませんが、
の範囲(投影された球面三角形の場合はこの範囲で十分)なら、
とすることができます。これが論文の擬似コード "Compute the third vertex of the sub-triangle." のところに対応します。
何が達成されたか?
上記の手法によって、単位面積の1軸が と結びつきました。これはイメージとしては、

このように面積を保存する形での対応が確立されたということになります。 ということは緯度については結局、経度について小さくスライスした領域について均一なマッピングを考えれば良いことになります。

となると、やはりこの図でいうところの y軸に対して均一にマッピングをすることになります。 ここについては、
の話と同じです。
 を求める
を求める
これを今までの球面三角形の文脈で考えてみます。
をちょうど 先の図で言うところのY軸であると捉えると、

を、上の図のちょうど赤の部分に均一にマッピングを考え、そこからPを生成すれば良さそうです。
ここで
に射影した
の位置は
ですので、

軸上での数値としては、1 から
に
のマッピングになるので、結局、
ここで は
であるので、
とも書くことができ、これが論文の擬似コード、"Use the other random variable to select cos θ." の部分になります。
zは一方で と捉えられるので、以下の図のように、

とPを構成できるため、結果、
これが論文の擬似コード、"Construct the corresponding point on the sphere." の部分になります。 以上で理論的な部分はすべてクリアになりました。
実装
以上をふまえて実装します。 三角形上の点が欲しかったので、この実装では平面の方程式と、光線の方程式の交点を追加で求めています。
比較
実際にパストレーシングに組み込んでみます。 ここでは、前回実装した、Spherical Rectangleと比較してみようと思います。MISを入れると差がわかりにくいため、MISなしのNext Event Estimation での比較になります。
ここでは2枚のポリゴンは等確率で選ばれています。
左がSpherical Triangle 、右がSpherical Rectangle になります。
わずかにSpherical Rectangleのほうが優れていることが確認できます。ただ、2つのポリゴンの選ばれ方を立体角に比例するように選ぶようにすれば、普通の一様乱数のケースでは少なくとも分散は等価ですし、例えばもう少し弱く、選択の重要度を、
※ を完全拡散面の放射輝度、Areaは三角形の面積、
を三角形の中心からサンプル元の距離とします。
といった形に定義して、この値に比例するようにサンプリングするようにしてみたりすると、
左がSpherical Triangle 、右がSpherical Rectangle になります。
これだけでも2つの差はかなり少なくなったように思います。もちろんメニーライトやら、不均一な放射輝度を持つポリゴンの場合やらを考えると、このような方法でカバーできる範疇を簡単にはみ出してしまいますが・・・。
まとめ
先にSpherical Trianglesではなく、Spherical Rectanglesをやったのは、単純な話 James Arvo, "Stratified Sampling of Spherical Triangles" の内容がよくわからなかったです(汗)。俯瞰してみると、球面三角形の式をとてもうまく使っていて、最終的には結構シンプルな形に帰着させており、よく思いつくものだとため息がでます。しかし天才的なひらめきが必要かというとそうでもない気もしました。自分でも思いつけるくらいになれたらと夢をみつつ・・・。導出には結構様々な小さなテクニックが使われていたので、追いかけるだけでも得られるものはあるのではないでしょうか。三角形ポリゴンということで、自前のレンダラーに組み込むにも便利ではないかと思います。
参考文献
James Arvo, "Stratified Sampling of Spherical Triangles"
Carlos Ureña, Marcos Fajardo, Alan King , “An Area-Preserving Parametrization for Spherical Rectangles”
張海潮, "球面三角形的AAA 定理"
An Area-Preserving Parametrization for Spherical Rectangles を読む
An Area-Preserving Parametrization for Spherical Rectangles
Carlos Ureña, Marcos Fajardo, Alan King , “An Area-Preserving Parametrization for Spherical Rectangles” は、
レイトレ合宿6 に提出しました MoodyRender で組み込んだものの、あまりしっかりとしたまとめを書いていませんでしたので、こちらにまとめておこうとおもいます。
こちらの論文は、SolidAngle社が EGSR 2013で発表した論文となっております。この論文では、単位面積 から、任意の長方形の領域を単位球面に射影してできた領域への写像を、面積を保存する形で提示します。文章で書くとややこしい印象になってしまいますが、イメージは以下のような感じです。

これは一度定義してしまえば、射影立体角内で、立体角一様なサンプルを生成したり、準乱数によるサンプルを生成したりも簡単にできます。このテクニックは特に直接照明の計算、いわゆるNext Event Estimationに便利です。
立体角でサンプリングしたくなる理由
Next Event Estimationを行う際、最も簡単なのは面積に一様なサンプルを生成することでしょう。しかしなぜわざわざややこしいことをして、立体角でサンプリングを生成するのでしょうか? 例えば以下のようなシチュエーションを考えてみましょう

これは結構横長な光源があり、そして手前側の半球の中心が現在光線追跡中の点で、ここの直接照明を考えるとしましょう。 面積に一様なサンプリングをした場合には赤い点のように生成されるでしょう。なんだか良さげですが、これを立体角に投射してみましょう。

...かなり偏っています。これが運良く、重点サンプリングのように機能するなら良いでしょうが、多くのシチュエーションではそんなことはないでしょう。これでは分散が増加してしまうのが目に見えています。なのでせめて立体角には一様なサンプリングをしたくなります。例えば以下のように。

そんなわけで、これをどのように達成しているのかを見ていきましょう。
写像
まず最初に面積を保存する写像とは何かを定義します。論文 3. Properties of map M では、以下のような式があります。
この式の意味を考えます。
ここではまず、単位面積の中の任意の領域 T を考えて、その面積を とします。

そして、写像する立体角の全領域をQ として、その立体角を とします。

そして T の写像を とすると、

全立体角あたりの、写像してきた立体角は、やはりTと一致する、これが面積を保存する写像というわけです。

座標系
次に座標系についてです。この論文では、もろもろ後の問題を単純にするために、長方形領域 P を基準にローカル座標系を定義します。 これは論文のFigure 1にあたります。
 ※ 元論文 Figure 1
※ 元論文 Figure 1
原点oを基準に、長方形 P 上にサンプルを生成するのをイメージします。 この座標系の重要なところは 、
の向きが x軸
の向きが y軸
- 長方形 P の原点o側の法線がz軸
となるような座標系であるというところです。
それぞれの軸の単位ベクトルは、長方形Pと、原点oが決まれば自動的に決まってくることになります。
ここでローカル座標系での そして
もやはり一意に決まりますので、ここで整理します。
sのローカル座標は、
であるので、座標軸に単に投射すれば良いため、 は、原点o から 長方形Pへのベクトルを d 、
を基底ベクトルとすると、
そしてそこから長方形のサイズ分ずらせば良いので は、
となります。
長方形の4点については重要な頂点になりますので、名前を と名前をつけておくことにします。

球面四角形の面積
ところで長方形の領域が射影された領域の立体角すなわち面積はどのように求めることができるでしょうか? 一般に単位球面三角形について、3つの角の角度から求めることができることが知られています。(証明は今回すっ飛ばします)

平面上の通常の三角形の内角の和はもちろん180° () でありますが、球面三角形の内角の和は膨らみがある分
以上になることは想像に難くないでしょう。
一方でこの式は、球面三角形の内角の和が
のときどうなるかというと、
面積が0になってしまいました。どういうことかといえば、球面三角形の内角の和が に近づいていくということは、それだけ平面上の三角形に近づいていくことであり、結局それは以下の図のようにどんどん小さくなっていってしまうわけです。

では逆に球面三角形の最大値はどんな値になるでしょうか?これを考えるために、上の図と"反対側"の球面三角形を考えてみます。

この場合、それぞれの外側の角度は、 となるわけなので、面積は、
となり、さらに の場合は、

のように小さくなっていき、式としても、
なるほど、単位球の表面積と一致しています。どうやらこれが最大値のようです。だいぶイメージも掴めてきました。 ところで、球面四角形の場合はどうかといえば、二つの球面三角形に分割して考えることができます。

したがって、
この時2つの角については、一つにまとめることができるので、
と4つの角の角度で考えることができます。
この角度で を再定義すると、

なんとシンプルでしょうか。これで立体角について簡単に考えていくことができそうです。 余談なのですが、ここまでの話は、自然に任意の球面N角形に拡張することができ、それはもちろん、
のようになります。 この拡張、以下のようにどこか適当な1点は実は球面N角形の1頂点だったと考えてみても、ちゃんと成り立ちます。
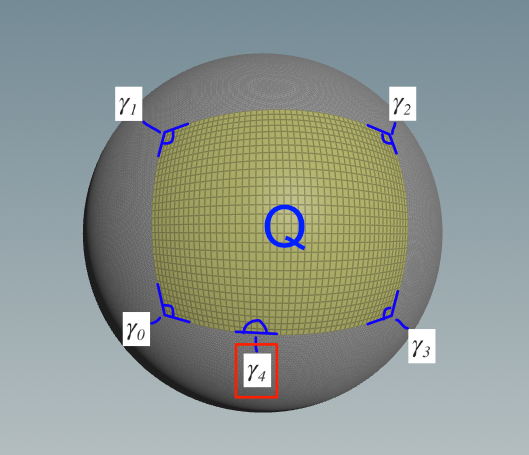
式の左の項を見ると、 N が1増えると面積は 増えそうですが、それは右側の項でちゃんと相殺されますね。
なかなか面白いものです。
 を求める
を求める
と立体角には密接な関係性があることがわかりました。そこで
をそれぞれ求めたいわけです。座標系のセクションですでに定義した、原点o と、
の4つの頂点で作られる平面の法線から考えます。


ベクトルの外積からそれぞれ、
のように求めることができると、図からわかります。
法線がわかってしまえば、 の値は、以下の図をみながら、

となります。
ここでついでにひとつ重要な話題があって、今回はローカル座標系としてうまいこと軸が長方形に整列した座標系を定義しました。

これを踏まえて面について後ろから観察すると、

と、このようになっています。このことから、
は Y軸にいつも直交しており、ローカル座標系でのy 成分は常に0
は X軸にいつも直交しており、ローカル座標系でのx 成分は常に0
であることがわかります。これは実装の最適化にも寄与します。
このことから、それぞれの法線はそれぞれ1つの角度の値で表現できることもわかります。


※元論文では、 だけなぜかマイナスで定義されています。理由がちょっと定かではないのですが、この部分はさほど重要な点ではないように思いましたので、ここではシンプルにすべて+での定義を使いました。
u 方向の累積分布関数
いよいよコア部分に入っていきます。単位面積におけるx座標を u 、y座標をvとパラメータ化することを考えます。

ここでは u について考えます。 uは当然 0 ~ 1 の間を行き来することになります。そのようなシチュエーションを考えた時、
のとき、
そして、
のとき、
もっと進んで、任意のuで、
が成り立つような を考えます。ここではこれは ローカル座標系でのxに対応させて考えると、

とこのような領域を定義したいです。 uについてアニメーションさせると、以下のようになるでしょう。

ただ多くのシチュエーションでは上の図のように綺麗な形をしておらず、例えば以下のように歪んでいるということは、一応確認しておきたいところです。例えば以下のように。

なのでuの値が線形に変化するとしても、当然面積が線形にはならないということです。
では の面積について考えてみます。元論文 Figure 2を見てみましょう。
今までの議論でイメージができていれば、とても立体的な図として見えるはずです。
 ※元論文 Figure 2
※元論文 Figure 2
この中で、多くのものは定義済みですが、以下青で丸をつけた部分については未定義でした。そして uに依存して変化する部分でもあります。

を計算したいということから考えると、
というのはやはり必要な値であり、それは
から求めます。
とは何か?といえば、uの値に応じて、
から
へ回転する法線であり、境界線の法線でもあります。
上から見るとわかりやすいです。

以上より、 の面積は以下のように書き下せることがわかります。
の角度パラメータ1つによる表現はすでに上の方で触れました。
これと同様に、 についてもやはり同様の表記が可能で、
と、このようになります。ここで、内積 と、
について考えてみます。
は今回のローカル座標系においては、
と、このような値になるでしょう。
同様に、 もローカル座標系においては、
となるわけです。つまり結局のところ、内積 と、
についてはローカル座標系でz成分のみの掛け算により、内積が得られます。
したがって、
は、
と記述することができ、元論文では、
とおいており、
と短く記述でき、さらに
から、
これが元論文の式 (8) になります。これはまるで逆関数法における、累積分布関数のようにも感じられるでしょう。 ちなみに、
は、
のローカル座標系のz成分
は、
のローカル座標系のz成分
であるとも整理できます。
次に は、まだこの段階ではどういった表現で得られるかはわかりませんが、仮に都合良く
が求まりさえすれば、射影する前の長方形の座標(ローカル座標系)の x成分
を得ることができます。
は、上から見ると、次の図のようになります。

したがって、これを90度回転させると、原点から境界線へと向かうベクトルが手に入ります。

ここで、長方形までの距離 と、 求めたい
は、次の図のような配置になっており、

したがって、
これで を得ることができました。
ただ、
については、 や、
では符号が逆になってしまうので、注意したいところではあります。

とはいえ、 は、明らかに、
なので、心配する必要はありませんでした。
というわけで、最終的には都合の良い を見つけることに焦点があたります。
※
と書いていますが、実際には
とuの関数として記述したほうが直観的かもしれません。
 を求める
を求める
こちらは元論文の Appendices, "A. Expressing cu as a function of u" の部分になります。
は定数であり、
だけが未知のため、これを求めることが目標となります。
論文の説明が十分わかりやすいので、ここはかなりストレートに追いかけます。
まず定数をまとめて表記を簡単にするため、関数 を導入します。
これにより、
はともにコサインであり、範囲は -1 ~ 1をはみ出ることはないので、

の中の引き算を外に引きずり出すため、ここで加法定理、
で、
すこし複雑化してしまいましたが、ここで、 は、

コサインからサインを求める形になるため、単位円の上半分を表しており、
から、

であり、とすると、
これを少し変形して、
こうすると、かなりの部分が から分離でき、
とおいてしまうと、
とかなり簡単になります。
あとは について解きます。ここも逆関数法みたいな香りがしますね。
おっと、符号が行方不明になってしまいました。 ただ、
をよく見ると、
なのは明らかです。したがって、 と
は同じ符号でなければなりません。
加えて、
であるため、以上をふまえると、 は、
であるべきでしょう。 長くなってしまったため、以上をまとめると、
となります。
 の除算について
の除算について
上記の式変形の中で、 で除算する部分があります。元論文中では、
は常に 0より小さいことが書かれています。しかしこれは事実ではありません。というのも、これの根拠にしているのが、
がそれぞれ
よりも大きいこと、と記述されておりますが、これが真実ではありません。反例として、例えば以下のようなシチュエーションがあります。

これは明らかに です。ということは自然と
も
となり得るということになります。
ただ、論文中で を示したかった理由は単にゼロ除算を避けるためにあります。
では実際にゼロ除算は実装上問題になるのでしょうか?
であるため、まず
になります。次に、
なので、
になります。最後に、
より、
そう、これは結局単に の地点であり、図示すると、

となり、異常な特異点というわけではないことがわかります。 ただ、ゼロ除算に近づいていく過程で0付近は数値的に誤差が生じやすいかもしれません。
この点については、知人の紹介で、Carlos Ureña氏とAlan King氏にメールで確認させて頂いたところ、確かにerrorであると確認していただけました。
なにが解決したか?
の
へのマッピングが以上で明らかになりました。これで何が実現できたのかを再確認します。
は連続的であり、イメージがややしにくいため、一旦均等に極めて細かく面積を分割することを考えます。
例えば極めて細かく、均等に4つに分割しますと、

この時立体角上に写像した a, b, c, dの面積(=立体角) も均等となります。
このようなマッピングが成立したことになります。
ということは、残る 方向については、以下のように経度方向に細かく分割した中で残りの縦方向の写像を考えれば良いことになります。

 のマッピングどうするか?
のマッピングどうするか?
ではここで、θに対して をマッピングするのは正しいでしょうか?

これは正しくありません。 なぜならθに均一に分割しても、それぞれの面積(=立体角)は一様ではないためです。 これは、
のような立体角積分でも として出現することからも明らかです。
これをなんとかするために、球とそれをすっぽりと覆う円柱の側面積の面積の関係性を使います。

ここでいう面積の関係性は、 横方向にスライスした部分の面積は、水平に切る限りどこでも一致する、というものです。(例えば赤い部分) ※これについて、単位球面に対してランダムに点を生成するでは、より詳細な説明をしています。
Y軸に対して面積は線形であり、そしてこの関係性は、経度方向に薄くスライスしても、同様の性質が保持されることは明らかです。さらに言えば、今回のケースは上下に切られている状況ではありますが、これも関係がありません。
ということは結局のところY軸に対して を線形にマッピングするだけで良いということになります。
 の詳細
の詳細
マッピングのアイディアがわかってしまえば、あとは幾何学的な部分を整理するだけになります。 元論文のFigure 3 を見てみましょう。
 ※元論文のFigure 3
※元論文のFigure 3
d は、xz平面上のp までの距離であり、
で求められます。
と
はどんな値かというと、oから
および
に向かうベクトルを正規化したあとのy成分で求めることができます。
ここの間を線形にマッピングすれば良いため、
と が 確定します。
ここから、
のときとほぼ同様に、

と を求めることができました。
グローバル座標へ
はローカル座標系での値ですので、最後にグローバル座標へ戻して終了です。
実装
以上を踏まえての実装です。
まずはナイーヴなほうです。
次に最適化したバージョンです。まだできることが残っていたらすみません。。
PathTracing + Next Event Estimation 比較
ナイーヴなPathTracing + Next Event Estimation の実装で、 面積に一様な場合 ( 64 spp ) と、立体角に一様な場合 ( 64 spp ) の比較です。
PathTracing + Next Event Estimation + MIS(パワーヒューリスティック) 比較
BRDFのサンプリングと光源のサンプリングの2戦略でのMISをした場合、 面積に一様な場合 ( 32 spp ) と、立体角に一様な場合 ( 32 spp ) の比較です。
MISなしのに比べると、差は少ないですが、確かにこの場合でも分散が低くなっています。特に光源付近では、MISウエイトによって分散の高いサンプルを十分に潰しきれていないことがわかります。
サンプリング生成コストが少し増加するので、同じsppで比較するのは完全にはフェアではありません。しかし単純なシーンならともかく、複雑なシーンではサンプリング生成コストの増加は相対的に影響度は少なく、この分散の低下のメリットが遥かに大きいと思います。 論文では、極めて最適化された実装で、プロダクションのシーンで、数パーセントのパフォーマンスの低下が見られたが、本手法のノイズ低減効果を考えると十分回収できるものだったとありました。
サンプリング手法と組み合わせる
また、今回の手法では、他のサンプリング手法と組み合わせるのが容易です。 例えばBlueNoiseのようなサンプリングからマッピングすると以下のような結果が得られます。


こちらのサンプルデモは以下にあります。
まとめ
この手法は、法線や頂点の数がそこそこ多く出てくる上、3Dなのでイメージするがやや難しいですが、実際にプロットしつつぐるぐる3Dビューを回して確認さえできれば、あとはそれほど高度な数学も登場してこないので、それほど難易度も高くなく、実装もシンプルで最適化もすれば十分効率的です。座標系のとりかたがうまいことがとても良く効いているように感じます。また分散低減は効果もわかりやすく、まだやったことがない方は試してみる価値は十分にあるのではないでしょうか。ただいったん三角形でいいや、という方は先行研究である、James Arvo, "Stratified sampling of spherical triangles" のほうを先に試したほうが良いかもしれません。ただ長方形の場合にそれを三角形二枚にしてサンプリングするのは、本手法と等価ではなく、論文によるとわずかに本手法のほうが分散が少ないようですね。
サンプリング対象が長方形限定であるのは、純粋にリミテーションであり、今後拡張される余地もあるでしょう。(もちろん三角形ポリゴンのバージョンはすでにありますが)また、cos項まで考慮したり、放射輝度が均一でない光源や、BSDFなども同時に考慮に入れれたら、さらにすごいかもしれません。
参考文献
Carlos Ureña, Marcos Fajardo, Alan King , “An Area-Preserving Parametrization for Spherical Rectangles”