Stratified Sampling of Spherical Trianglesを読む

Stratified Sampling of Spherical Triangles

元論文は、James Arvo, "Stratified Sampling of Spherical Triangles" で、前回のこちらの関連になります。

ushiostarfish.hatenablog.com

James Arvo, "Stratified Sampling of Spherical Triangles" は、Spherical Rectanglesよりもだいぶ前の論文で、SIGGRAPH '95 の論文とのことです。Carlos Ureña, Marcos Fajardo, Alan King , “An Area-Preserving Parametrization for Spherical Rectangles” からも当然引用があります。

こちらもやはりモチベーションや達成したい目的は同じで、単位面積 $\left[0\, 1 \right]^2$ から、任意の 三角形 の領域を単位球面に射影してできた領域への写像を、面積を保存する形で提示します。

球面三角法

やはりこの論文でも、球面三角形の性質をうまく使っていきます。まずは前回も登場した、単位球面三角形の面積と頂点の角度の関係式、

f:id:ushiostarfish:20181021145939p:plain

$\displaystyle { Area =\alpha+\beta+\gamma-\pi }$

そして、もう一つ単位球面三角形の角度の余弦定理と呼ばれる式、

f:id:ushiostarfish:20181021145820p:plain

※a, b, cは球面上の線の弧の長さです

$\displaystyle { \cos { \beta } =-\cos { \gamma } \cos { \alpha } +\sin { \gamma } \sin { \alpha } \cos { b } \\ \cos { \gamma } =-\cos { \beta } \cos { \alpha } +\sin { \beta } \sin { \alpha } \cos { c } }$

が論文中の(1) ~ (3)にあります。

(1) については、前回触れていたので省略します。

また、導出については、

risalc.info

の説明が大変わかりやすく、オススメです。

しかし、単位球面三角形の角度の余弦定理についてはなんぞこれ？という感じがします。イマイチイメージしずらいのですが、ちょっと特殊なケースについて試してみましょう。例えば $\alpha=\frac {\pi} {2}$ かつ $\gamma=\frac {\pi} {2}$ のケースです。この時は以下のようなシチュエーションになるでしょう。

f:id:ushiostarfish:20181021161736p:plain

赤い線を赤道だとすると、 $\beta$ の頂点はちょうど北極点（南極点）に位置します。これは、先に $\beta$ が決まっていたとして、 $\alpha=\frac {\pi} {2}$ かつ $\gamma=\frac {\pi} {2}$ となるように線を引くとしたら以下のようにやはり真ん中を選ぶしか無いから、と考えると直観的です。

f:id:ushiostarfish:20181021162627p:plain

では式はどうなるかというと、

$\displaystyle { \cos { \beta } =-\cos { \gamma } \cos { \alpha } +\sin { \gamma } \sin { \alpha } \cos { b } \\ \cos { \beta } =-\cos { \frac { \pi }{ 2 } } \cos { \frac { \pi }{ 2 } } +\sin { \frac { \pi }{ 2 } } \sin { \frac { \pi }{ 2 } } \cos { b } \\ \cos { \beta } =\cos { b } }$

$b$ と $\beta$ が直接結びつく形になりました。これはある意味当たり前で、赤道の長さが $2\pi$ なので、 $b$ は、

$\displaystyle { b=2\pi \frac { \beta }{ 2\pi } \\ b=\beta }$

となるからです。ちょっとだけ親近感が湧いてきました。このように単位球面三角形の角度の余弦定理は、ある１辺の長さと三角形の角度を繋げてくれるものだと言えます。では一緒に導出のほうも見てみることにします。

これについては、張海潮氏の、"球面三角形的AAA 定理" にわかりやすい解説があったのでこちらを見てみることにします。中国語ですが、google 翻訳があれば結構大丈夫です。

圖二（図２）の下を見てみます。

f:id:ushiostarfish:20181021164450p:plain

※張海潮, "球面三角形的AAA 定理" 圖二より

記号については同じものを使っているので、混乱しなくて助かります。 $l, m, n$ はそれぞれ球の切り口の法線になります。ここで２つのベクトル $n\times l$ と $n\times m$ を考えます。これはそれぞれ、球心からAに向かうべクトル、球心からCに向かうべクトルと向きが一致します。図にすると、

f:id:ushiostarfish:20181021165929p:plain

※長さは適当です

この時、さらにこの２つのベクトルの内積を考えます。

$\displaystyle { \left( n\times l \right) \cdot \left( n\times m \right) }$

これは幸運にもスカラー４重積の形をしており、

$\displaystyle { \left( n\times l \right) \cdot \left( n\times m \right) =det\begin{pmatrix} n\cdot n & n\cdot m \\ l\cdot n & l\cdot m \end{pmatrix}=det\begin{pmatrix} 1 & \cos { \gamma } \\ -\cos { \alpha } & \cos { \beta } \end{pmatrix}=\cos { \beta } +\cos { \gamma } \cos { \alpha } }$

うまいこと球面三角形の角度だけで表すことができます。他方、内積の定義、 $\overrightarrow { a } \cdot \overrightarrow { b } =|\overrightarrow { a } ||\overrightarrow { b } |\cos \theta$ から考えると、

$\displaystyle { \left( n\times l \right) \cdot \left( n\times m \right) =\left| n\times l \right| \left| n\times m \right| \cos \theta }$

ここで $\theta$ は∠AOCの角度であり、ということはつまり bの長さでもあります。そして単位ベクトルの外積のベクトルの長さは $\sin$ を使っても表せるので、これらを利用すると、

$\displaystyle { \left| n\times l \right| \left| n\times m \right| \cos \theta =\sin { \alpha } \sin { \gamma } \cos b }$

以上２つの式をつなげると、

$\displaystyle { \cos { \beta } +\cos { \gamma } \cos { \alpha } =\sin { \gamma } \sin { \alpha } \cos b }$

となり、これが元論文の式 (2) に対応します。論文には２つしか書かれていませんが、当然３つ式を考えることができます。

$\displaystyle { \cos { \alpha } +\cos { \beta } \cos { \gamma } =\sin { \beta } \sin { \gamma } \cos a\\ \cos { \beta } +\cos { \gamma } \cos { \alpha } =\sin { \gamma } \sin { \alpha } \cos b\\ \cos { \gamma } +\cos { \alpha } \cos { \beta } =\sin { \alpha } \sin { \beta } \cos c }$

なかなか綺麗なものです。

The Sampling Algorithm

上記の式を使って、実際にサンプリングについて考えていきます。本手法でも、前回と同じく２段階のアルゴリズムになっています。論文 Figure1を見てみましょう。

f:id:ushiostarfish:20181021175259p:plain

※James Arvo, "Stratified Sampling of Spherical Triangles" Figure 1 より

１段階目で $AC$ 上の $\hat { C }$ を選択、２段階目で $B\hat { C }$ 上の $P$ を選択する、といった具合です。まずは１段階目から参ります。ここでは球面三角形 $AB\hat { C }$ に着目して、先程の球面三角形の角度の余弦定理のうち、 $\hat { C }$ を決めるのに重要な量、 $\hat{b}, \beta$ の両方が組み込まれている、

$\displaystyle { \cos { \hat { \beta } } =-\cos { \hat { \gamma } } \cos { \alpha } +\sin { \hat { \gamma } } \sin { \alpha } \cos { \hat { b } } }$

この式を出発点として考えてみます。ここで、球面三角形 $ABC$ の面積を $I$ 、球面三角形 $AB\hat { C }$ の面積を $\hat{I}$ とおくと、

$\displaystyle { \hat { I } =\alpha +\hat { \beta } +\hat { \gamma } -\pi \\ \hat { \gamma } =\hat { I } -\alpha -\hat { \beta } +\pi }$

※面積の記号として $I$ については、論文と違います。論文の記号がAとかぶってややこしいからです。

これを使うと、 $\hat{ \gamma }$ をうまく置き換えることができ、

$\displaystyle { \cos { \hat { \beta } } =-\cos { \left( \hat { I } -\alpha -\hat { \beta } +\pi \right) } \cos { \alpha } +\sin { \left( \hat { I } -\alpha -\hat { \beta } +\pi \right) } \sin { \alpha } \cos { \hat { b } } \\ \cos { \hat { \beta } } =\cos { \left( \hat { I } -\alpha -\hat { \beta } \right) } \cos { \alpha } -\sin { \left( \hat { I } -\alpha -\hat { \beta } \right) } \sin { \alpha } \cos { \hat { b } } }$

ここで一旦、 $\phi =\hat { I } -\alpha$ とおくと、

$\displaystyle { \cos { \hat { \beta } } =\cos { \left( \phi -\hat { \beta } \right) } \cos { \alpha } -\sin { \left( \phi -\hat { \beta } \right) } \sin { \alpha } \cos { \hat { b } } \\ \cos { \hat { \beta } } -\cos { \left( \phi -\hat { \beta } \right) } \cos { \alpha } =-\sin { \left( \phi -\hat { \beta } \right) } \sin { \alpha } \cos { \hat { b } } \\ \frac { \cos { \left( \phi -\hat { \beta } \right) } \cos { \alpha } -\cos { \hat { \beta } } }{ \sin { \left( \phi -\hat { \beta } \right) } \sin { \alpha } } =\cos { \hat { b } } }$

これが論文の式 (4)になります。

写像元の単位面積 $\left[0\, 1 \right]^2$ の１つ目の変数を $\xi _{ u }$ とすると、

$\displaystyle { I\xi _{ u }=\hat { I } }$

であることもついでに確認しておきます。

ここでポイントなのは、 $\xi _{ u }$ が定まると、 $\hat{I}$ が定まり、 $\phi$ が決まり、自動的に $\cos \hat {b}$ が定まる、そうすれば $\hat{C}$ が定まりそうです。ただ論文の式 (4)にはまだ問題があって、 $\hat{\beta}$ が残ってしまっています。本当はこの項は自動的に決まるはずであり、なんとか消したいと考えます。

ここで球面三角形 $AB\hat { C }$ で球面三角形の角度の余弦定理をもう１パターン持ってきます。

$\displaystyle { \cos { \hat { \gamma } } =-\cos { \hat { \beta } } \cos { \alpha } +\sin { \hat { \beta } } \sin { \alpha } \cos { c } }$

これは論文の式(3)に対応します。この式に対して同様の操作をしてみます。

$\displaystyle { \begin{eqnarray} \cos { \hat { \gamma } } & = & -\cos { \hat { \beta } } \cos { \alpha } +\sin { \hat { \beta } } \sin { \alpha } \cos { c } \\ \cos { \left( \hat { I } -\alpha -\hat { \beta } +\pi \right) } & = & -\cos { \hat { \beta } } \cos { \alpha } +\sin { \hat { \beta } } \sin { \alpha } \cos { c } \\ -\cos { \left( \hat { I } -\alpha -\hat { \beta } \right) } & = & -\cos { \hat { \beta } } \cos { \alpha } +\sin { \hat { \beta } } \sin { \alpha } \cos { c } \\ -\cos { \left( \phi -\hat { \beta } \right) } & = & -\cos { \hat { \beta } } \cos { \alpha } +\sin { \hat { \beta } } \sin { \alpha } \cos { c } \\ \cos { \left( \phi -\hat { \beta } \right) } & = & \cos { \hat { \beta } } \cos { \alpha } -\sin { \hat { \beta } } \sin { \alpha } \cos { c } \end{eqnarray} }$

ここで加法定理でさらに続けて、

$\displaystyle { \begin{eqnarray} \cos { \phi } \cos { \hat { \beta } } +\sin { \phi } \sin { \hat { \beta } } &=&\cos { \hat { \beta } } \cos { \alpha } -\sin { \hat { \beta } } \sin { \alpha } \cos { c } \\ \cos { \phi } \cos { \hat { \beta } } +\sin { \phi } \sin { \hat { \beta } } -\cos { \hat { \beta } } \cos { \alpha } +\sin { \hat { \beta } } \sin { \alpha } \cos { c } &=&0\\ \cos { \phi } \cos { \hat { \beta } } -\cos { \hat { \beta } } \cos { \alpha } +\sin { \phi } \sin { \hat { \beta } } +\sin { \hat { \beta } } \sin { \alpha } \cos { c } &=&0\\ \left( \cos { \phi } -\cos { \alpha } \right) \cos { \hat { \beta } } +\left( \sin { \phi } +\sin { \alpha } \cos { c } \right) \sin { \hat { \beta } } &=&0 \end{eqnarray} }$

ここで一旦 $\beta$ に集中するため、以下のように、

$\displaystyle { u=\cos { \left( \phi \right) } -\cos { \left( \alpha \right) } \\ v=\sin { \left( \phi \right) } -\sin { \left( \alpha \right) } \cos { \left( c \right) } }$

とおくと、

$\displaystyle { u\cos { \left( \hat { \beta } \right) } +v\sin { \left( \hat { \beta } \right) } =0 }$

とシンプルにまとめることができました。さらにここで、

$\displaystyle { \sin { x } =\sqrt { 1-\cos ^{ 2 }{ x } } }$

の関係を使って、

$\displaystyle { u\cos { \left( \hat { \beta } \right) } \pm v\sqrt { 1-\cos ^{ 2 }{ \hat { \beta } } } =0 }$

ただ、符号については $\beta$ によって変えなければなりません。

f:id:ushiostarfish:20181021185020p:plain

そのことを一旦 $\pm$ と記述することにしますが、次に、

$\displaystyle { \left( u\cos { \left( \hat { \beta } \right) } \pm v\sqrt { 1-\cos ^{ 2 }{ \hat { \beta } } } \right) \left( u\cos { \left( \hat { \beta } \right) } \mp v\sqrt { 1-\cos ^{ 2 }{ \hat { \beta } } } \right) =0 }$

のように符号と逆になった項をかけます。すると、

$\displaystyle { u\cos { \left( \hat { \beta } \right) } \pm v\sqrt { 1-\cos ^{ 2 }{ \hat { \beta } } } =0\\ \left( u\cos { \left( \hat { \beta } \right) } \pm v\sqrt { 1-\cos ^{ 2 }{ \hat { \beta } } } \right) \left( u\cos { \left( \hat { \beta } \right) } \mp v\sqrt { 1-\cos ^{ 2 }{ \hat { \beta } } } \right) =0\\ { u }^{ 2 }\cos ^{ 2 }{ \hat { \beta } } -{ v }^{ 2 }\left( 1-\cos ^{ 2 }{ \hat { \beta } } \right) =0\\ { u }^{ 2 }\cos ^{ 2 }{ \hat { \beta } } -{ v }^{ 2 }+{ v }^{ 2 }\cos ^{ 2 }{ \hat { \beta } } =0\\ { u }^{ 2 }\cos ^{ 2 }{ \hat { \beta } } +{ v }^{ 2 }\cos ^{ 2 }{ \hat { \beta } } ={ v }^{ 2 }\\ \left( { u }^{ 2 }+{ v }^{ 2 } \right) \cos ^{ 2 }{ \hat { \beta } } ={ v }^{ 2 }\\ \cos ^{ 2 }{ \hat { \beta } } =\frac { { v }^{ 2 } }{ { u }^{ 2 }+{ v }^{ 2 } } \\ \cos { \hat { \beta } } =\frac { \pm v }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } }$

結果的に最初の部分の符号については気にする必要はない状態で $\cos \hat {\beta}$ を得る事ができました。結局最後は符号が行方不明になってしまいましたが...。

$\sin$ についても同様の操作を行うと、

$\displaystyle { v\sin { \left( \hat { \beta } \right) } \pm u\sqrt { 1-\sin ^{ 2 }{ \hat { \beta } } } =0\\ \left( v\sin { \left( \hat { \beta } \right) } \pm u\sqrt { 1-\sin ^{ 2 }{ \hat { \beta } } } \right) \left( v\sin { \left( \hat { \beta } \right) } \mp u\sqrt { 1-\sin ^{ 2 }{ \hat { \beta } } } \right) =0\\ { v }^{ 2 }\sin ^{ 2 }{ \hat { \beta } } -{ u }^{ 2 }\left( 1-\sin ^{ 2 }{ \hat { \beta } } \right) =0\\ { v }^{ 2 }\sin ^{ 2 }{ \hat { \beta } } -{ u }^{ 2 }+{ u }^{ 2 }\sin ^{ 2 }{ \hat { \beta } } =0\\ { v }^{ 2 }\sin ^{ 2 }{ \hat { \beta } } +{ u }^{ 2 }\sin ^{ 2 }{ \hat { \beta } } ={ u }^{ 2 }\\ \left( { v }^{ 2 }+{ u }^{ 2 } \right) \sin ^{ 2 }{ \hat { \beta } } ={ u }^{ 2 }\\ \sin ^{ 2 }{ \hat { \beta } } =\frac { { u }^{ 2 } }{ { u }^{ 2 }+{ v }^{ 2 } } \\ \sin { \hat { \beta } } =\frac { \pm u }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } }$

と、 $\sin \hat {\beta}$ についても、符号はともかく得ることができました。

さて、

$\displaystyle { u\cos { \left( \hat { \beta } \right) } +v\sin { \left( \hat { \beta } \right) } =0 }$

をちょっとだけ変形してみると、

$\displaystyle { u\cos { \hat { \beta } } =-v\sin { \hat { \beta } } \\ \frac { \cos { \hat { \beta } } }{ v } =-\frac { \sin { \hat { \beta } } }{ u } }$

ここからわかることは、 $\frac { \cos { \hat { \beta } } }{ v }$ と $\frac { \sin { \hat { \beta } } }{ u }$ は常に符号が逆にならなければならない、ということです。それを踏まえて、 $\cos \hat {\beta}$ と $\sin \hat {\beta}$ についても少しだけ変形してみると、

$\displaystyle { \pm \frac { \sin { \hat { \beta } } }{ u } =\frac { 1 }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } \\ \pm \frac { \cos { \hat { \beta } } }{ v } =\frac { 1 }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } }$

のようになります。ここで、 $\frac { \cos { \hat { \beta } } }{ v }$ が負のケースを考えてみると、両方とも右辺は常に正であることが求められますので、

$\displaystyle { +\frac { \sin { \hat { \beta } } }{ u } =\frac { 1 }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } \\ -\frac { \cos { \hat { \beta } } }{ v } =\frac { 1 }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } }$

逆に $\frac { \sin { \hat { \beta } } }{ u }$ が負のケースは、

$\displaystyle { -\frac { \sin { \hat { \beta } } }{ u } =\frac { 1 }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } \\ +\frac { \cos { \hat { \beta } } }{ v } =\frac { 1 }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } }$

つまり結局のところ、

$\displaystyle { \sin { \hat { \beta } } =\frac { \mp u }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } \\ \cos { \hat { \beta } } =\frac { \pm v }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } }$

のように $\cos \hat {\beta}$ と $\sin \hat {\beta}$ の符号はお互いに逆になるということになります。 ※実際には $\beta$ によって符号がフリップしますが、後の議論によってさほど本質的は問題ないことがわかります。

これを使って、少し戻ってしまいますが、論文の式(4)

にこれを代入していきます。

$\displaystyle { \cos { \hat { b } } =\frac { \cos { \left( \phi -\hat { \beta } \right) } \cos { \alpha } -\cos { \hat { \beta } } }{ \sin { \left( \phi -\hat { \beta } \right) } \sin { \alpha } } \\ \cos { \hat { b } } =\frac { \left( \cos { \phi } \cos { \hat { \beta } } +\sin { \phi } \sin { \hat { \beta } } \right) \cos { \alpha } -\cos { \hat { \beta } } }{ \left( \sin { \phi } \cos { \hat { \beta } } -\cos { \phi } \sin { \hat { \beta } } \right) \sin { \alpha } } \\ \cos { \hat { b } } =\frac { \left( \cos { \phi } \frac { \pm v }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } +\sin { \phi } \frac { \mp u }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } \right) \cos { \alpha } -\frac { \pm v }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } }{ \left( \sin { \phi } \frac { \pm v }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } -\cos { \phi } \frac { \mp u }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } } \right) \sin { \alpha } } \\ \cos { \hat { b } } =\frac { \left( \pm v\cos { \phi } \mp u\sin { \phi } \right) \cos { \alpha } \mp v }{ \left( \pm v\sin { \phi } \pm u\cos { \phi } \right) \sin { \alpha } } \\ \cos { \hat { b } } =\frac { \pm \left( v\cos { \phi } -u\sin { \phi } \right) \cos { \alpha } \mp v }{ \pm \left( v\sin { \phi } +u\cos { \phi } \right) \sin { \alpha } } \\ \cos { \hat { b } } =\frac { \pm \left\{ \left( v\cos { \phi } -u\sin { \phi } \right) \cos { \alpha } -v \right\} }{ \pm \left( v\sin { \phi } +u\cos { \phi } \right) \sin { \alpha } } \\ \cos { \hat { b } } =\frac { \left( v\cos { \phi } -u\sin { \phi } \right) \cos { \alpha } -v }{ \left( v\sin { \phi } +u\cos { \phi } \right) \sin { \alpha } } }$

なんと、都合の良いことに、正負が打ち消し合って綺麗に消えてくれました。これが論文の式 (5) ということになります。最後の代入のおかげで、 $\beta$ は完全に姿を消し、写像元の単位面積 $\left[0\, 1 \right]^2$ の１つ目の変数 $\xi _{ u }$ からダイレクトに $\cos \hat{b}$ へと繋げる事ができました。

$\hat { C }$ を求める

$\cos \hat{b}$ が求まりましたので、次に実際にそこから $\hat { C }$ の値を求めていきます。論文では記述の簡略化のために、以下の表記を使っています。

$\displaystyle { \left[ x|y \right] =normalize \left( x-\left( x\cdot y \right) y \right) }$

※ ここで yは単位ベクトルとします

これは、どういう演算かというと、

f:id:ushiostarfish:20181024214549p:plain

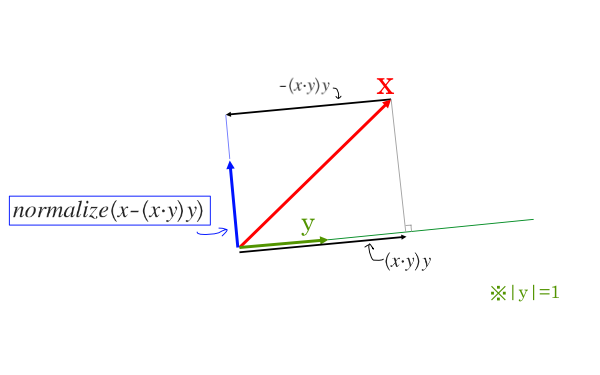
そう、x方向の、yと直交するベクトルを得る演算ということになります。これを使えば、AからCに向かっての回転を簡単に考えることができます。

f:id:ushiostarfish:20181024223531p:plain

※もちろん、実装上クォータニオンなどを使って回転させるのも可能だと思いますが、こちらのやり方のほうがシンプルなように思いました。

また、今手元には $\cos \hat{b}$ しかありませんが、 $0 \le \hat{b} \le \pi$ の範囲（投影された球面三角形の場合はこの範囲で十分）なら、

$\displaystyle { \hat { C } =A\cos { \hat{b} } +\left[ C|A \right] \sqrt { 1-\cos ^{ 2 }{ \hat{b} } } }$

とすることができます。これが論文の擬似コード "Compute the third vertex of the sub-triangle." のところに対応します。

何が達成されたか？

上記の手法によって、単位面積の１軸が $\hat{b}$ と結びつきました。これはイメージとしては、

f:id:ushiostarfish:20181027131229p:plain

このように面積を保存する形での対応が確立されたということになります。ということは緯度については結局、経度について小さくスライスした領域について均一なマッピングを考えれば良いことになります。

f:id:ushiostarfish:20181027133151p:plain

となると、やはりこの図でいうところの y軸に対して均一にマッピングをすることになります。ここについては、

ushiostarfish.hatenablog.com

の話と同じです。

$P$ を求める

これを今までの球面三角形の文脈で考えてみます。 $B$ をちょうど先の図で言うところのY軸であると捉えると、

f:id:ushiostarfish:20181027135945p:plain

$\xi_v$ を、上の図のちょうど赤の部分に均一にマッピングを考え、そこからPを生成すれば良さそうです。ここで $B$ に射影した $\hat {C}$ の位置は $\cos { \theta _{ \hat { C } } }$ ですので、

f:id:ushiostarfish:20181027142339p:plain

$B$ 軸上での数値としては、1 から $\cos { \theta _{ \hat { C } } }$ に $\xi_v$ のマッピングになるので、結局、

$\displaystyle { z=1+\xi _{ v }\left( 1- \cos { \theta _{ \hat { C } } } \right) }$

ここで $\cos { \theta _{ \hat { C } } }$ は $\hat { C } \cdot B$ であるので、

$\displaystyle { z=1+\xi _{ v }\left( 1-\hat { C } \cdot B \right) }$

とも書くことができ、これが論文の擬似コード、"Use the other random variable to select cos θ." の部分になります。 zは一方で $\cos \theta$ と捉えられるので、以下の図のように、

f:id:ushiostarfish:20181027142700p:plain

とPを構成できるため、結果、

$\displaystyle { P=\cos { \theta } B+\sin { \theta } \left[ \hat { C } |B \right] \\ P=\cos { \theta } B+\sqrt { 1-\cos ^{ 2 }{ \theta } } \left[ \hat { C } |B \right] \\ P=zB+\sqrt { 1-{ z }^{ 2 } } \left[ \hat { C } |B \right] }$

これが論文の擬似コード、"Construct the corresponding point on the sphere." の部分になります。以上で理論的な部分はすべてクリアになりました。

実装

以上をふまえて実装します。三角形上の点が欲しかったので、この実装では平面の方程式と、光線の方程式の交点を追加で求めています。

比較

実際にパストレーシングに組み込んでみます。ここでは、前回実装した、Spherical Rectangleと比較してみようと思います。MISを入れると差がわかりにくいため、MISなしのNext Event Estimation での比較になります。

ここでは２枚のポリゴンは等確率で選ばれています。

左がSpherical Triangle 、右がSpherical Rectangle になります。

わずかにSpherical Rectangleのほうが優れていることが確認できます。ただ、２つのポリゴンの選ばれ方を立体角に比例するように選ぶようにすれば、普通の一様乱数のケースでは少なくとも分散は等価ですし、例えばもう少し弱く、選択の重要度を、

$\displaystyle { w=L\frac { Area }{ d^{ 2 }\left( o,TriangleCenter \right) } }$

※ $L$ を完全拡散面の放射輝度、Areaは三角形の面積、 $d\left( o,TriangleCenter \right)$ を三角形の中心からサンプル元の距離とします。

といった形に定義して、この値に比例するようにサンプリングするようにしてみたりすると、

左がSpherical Triangle 、右がSpherical Rectangle になります。

これだけでも２つの差はかなり少なくなったように思います。もちろんメニーライトやら、不均一な放射輝度を持つポリゴンの場合やらを考えると、このような方法でカバーできる範疇を簡単にはみ出してしまいますが・・・。

まとめ

先にSpherical Trianglesではなく、Spherical Rectanglesをやったのは、単純な話 James Arvo, "Stratified Sampling of Spherical Triangles" の内容がよくわからなかったです（汗）。俯瞰してみると、球面三角形の式をとてもうまく使っていて、最終的には結構シンプルな形に帰着させており、よく思いつくものだとため息がでます。しかし天才的なひらめきが必要かというとそうでもない気もしました。自分でも思いつけるくらいになれたらと夢をみつつ・・・。導出には結構様々な小さなテクニックが使われていたので、追いかけるだけでも得られるものはあるのではないでしょうか。三角形ポリゴンということで、自前のレンダラーに組み込むにも便利ではないかと思います。