2018-09-09

レイトレ合宿６に行ってきました

島です！

f:id:ushiostarfish:20180908173421j:plain

今年は神津島です。島にくると旅行している感が圧倒的で、テンションは爆上がりですね！（天候で帰れないリスクとかありますけど・・・延泊組は台風の影響が少し心配されましたが、全員無事帰ってこれたようです）自分は朝のジェット船組だったので、１日目は温泉にひとまず入ったらすぐメインイベントへ

あとまったく知らなかったのですが、丁度その日に第1回神津島アクアスロンなるイベントが昼にあったらしく、

第７回神津島アクアスロン大会が開催されました。 - 本日の神津島

温泉の場所から、レイトレ合宿イベント会場までの道路も封鎖される！！！ということで少し焦りつつレンタルサイクルを飛ばしました。（間に合ったはずだったんですが、結局みんなが遅れているのをいいことにフランクフルトを買っていて遅刻しちゃいましたが・・・すみません！

レイトレ検定

偉人Tシャツシリーズのおかげで、Ivan Edward Sutherlandを選ぶ問題は楽勝だったものの、結構わからない問題も。ぐやじい('ᾥ' )。レイトレ合宿はラスタライザを滅ぼしリアルタイムレイトレーシングを実現することだったのか・・・精神を高めるためだと思ってた・・・

ところで、来年はぜひ三葉レイちゃんTシャツが欲しいです！よろしくお願いします！

参加していない方も、レイトレ合宿6 に問題と回答があるのでレイトレが好きな人は楽しめると思います。

三葉レイちゃんの応援メッセージ

f:id:ushiostarfish:20180908180758j:plain ※レイトレ合宿6 サイトより

なんと、特別に応援動画をいただいていたとのこと！かわいい。なにか絡みがあるんじゃないかと前々から思ってはいましたが、驚きました！もちろん中の人などいないのですが、マネージャー的な人は現地参加者の中にいるんじゃないかと思っていたものの、どうやらそうでもないようです。かわいい

セミナー

Zinさんおよびishiyamaさんによる発表がありました。Zinさんの発表でのレンダラーのテストの話は、わりと頭の痛い問題だなぁ・・・と思います。特に組み合わせで発生するような問題をあぶり出すために、うまいテストを作りたい、というのはレンダラー開発だけで起こる問題ではないようにも思いました。 ishiyamaさんの発表では、ボリュームレンダリング方程式にいくつかの仮定をおくことで大気拡散のモデルを導出するというものでしたが、高度すぎて自分はポカーン状態でしたが、ざっくりと考え方や雰囲気を追うだけでも勉強になりました。こんなふうに自在に理論を操ることができれば、やれることの自由度がぐっと上がりそうで、それはとても良いことだなぁと思いました。ずっと自分はボリュームレンダリングはほったらかしだったので、そのうちチャレンジしたいとは思っています。holeさんによると、

cs.dartmouth.edu

がサーベイとしてとても良いとのことだったので、後ほどチャレンジしたいです。

発表

今回の自分の最終絵はこちらです。 f:id:ushiostarfish:20180908180505p:plain フルHD(1920x1080) のおそらく520sppいかないくらいで終了だと思います。（embree、ポリゴン超多くてもパフォーマンスめちゃくちゃ良くてびっくりです。

そして３位の景品をいただきました！ありがとうございます！本だけどカメラ・・・カメラなのに本です。近い内に試したいですね！

カメラを賞品としていただきました！？これでカメラ完全に理解しちゃいます！#レイトレ合宿6 pic.twitter.com/xHnKvqO8Q3
— うしお (@ushiostarfish) 2018年9月1日

スライドとソースコードはこちらです。

スライドとhttps://t.co/MMhaeQ3bAD
ソースコードです！https://t.co/ShVxPJZ3su #レイトレ合宿6
— うしお (@ushiostarfish) 2018年9月4日

※ベルベットですが、ラフネスがわりと低い割にエッジの光り方が弱い気がするがちょっときになるところで、後ほど追加検証せねば・・・

あんまり尖ったことは盛り込めなかった反面、houdiniとかembreeとかうまく噛み合ってすごく開発はやりやすかったところは良かったです。来年加速データ構造をどうするかはちょっと悩みますね...それこそRTXに乗っかるならそれもいいのかもしれませんが、embree爆速だったとはいえずっとembreeというのも味気ない...

ところで、NUMA(Non-Uniform Memory Access)により半分しかうまくCPUを使えない！！問題がwindowsであったようなのですが、TBBのおかげか、自分のケースでは特に意識することなく妥当な並列性能だったように思いました。どうやらTBB 3.0からは透過的に扱えるになっているらしいです。

software.intel.com

しかし、今年もみんなそれぞれ違ったチャレンジがあり、すごい！ 目立つところだと、光源をガラスの中に閉じ込めるハードモードをやったり、VCMへのチャレンジや、メニーライト、Full-Featured with RTX、大気拡散...などなどアドベントカレンダーもどれも勉強になるものばかりです。調べたり勉強したり試したり、そしてそれが共有されて、みなが先生であり生徒になっていけば、きっとガンガン加速していきそうです。（ちょっと意識すぎるコメントになってしまいました。

シーンについて

スライドではあんまり詳しくシーンの作りについては共有しておりませんでしたので、こちらに自分の備忘録としても良いので乗っけておこうとおもいました。

イルカ

イルカについてはまずblenderでMirrorモディファイアとSubdivision Surfaceモディファイアを適用しつつ手作業でモデルを作成します。 f:id:ushiostarfish:20180909190535p:plain blender 上でdeformモディファイアとかで曲げても良かったのかもしれませんが、今回はhoudiniをいろいろ使っていきたかったので、この時点でhoudiniに持っていきます。

Houdiniに持ってきたら、Wire Captureをして、 f:id:ushiostarfish:20180909191238p:plain

ラインをBendしたものを用意して、 f:id:ushiostarfish:20180909191336p:plain

Wire Deformを適用します。 f:id:ushiostarfish:20180909191425p:plain

波

Curveでまず１区画を作ります。 f:id:ushiostarfish:20180909191837p:plain

いったんゴニョゴニョやってメッシュ化します。縦には細かく刻んであるのは曲げても破綻しにくくするためです。 f:id:ushiostarfish:20180909191957p:plain

LineとCopy to Pointsを使って繰り返します。 f:id:ushiostarfish:20180909192217p:plain

Vexプログラミングで丸くします。 f:id:ushiostarfish:20180909192315p:plain

押し出したり、Fuseでつなげたり法線を調整したりして完成です。 f:id:ushiostarfish:20180909192413p:plain

Houdiniのよく挙げられる良いところは非破壊なところで、一番最初のカーブまで戻って修正が可能なところです f:id:ushiostarfish:20180909192714g:plain

リング

まずはラインを用意して、 f:id:ushiostarfish:20180909193010p:plain

すごく適当にランダムに動かしつつ、法線とスケールをすごく適当に設定します。このとき微妙に配置が気にいらないときは、乱数シードをずらしてかっこいいのを探します。数十個程度パラパラと見れば良いシードが見つかるものです。 f:id:ushiostarfish:20180909193042p:plain

Copy To Pointsでサークルを配置して、 f:id:ushiostarfish:20180909193135p:plain

Poly Wireで厚さをつくって、 f:id:ushiostarfish:20180909193235p:plain

ポリゴンがめり込んでいるのは今回は嫌だったので、一度VDB from PolygonsとConvertで一度vdbを経由することで、めり込みを回避しつつリングの境界線をなめらかにします。 f:id:ushiostarfish:20180909193334p:plain

あとは外側のリングを適当に配置して完成です。 f:id:ushiostarfish:20180909193604p:plain

クロス

まず適当な粗さでグリッドを用意しつつ、Cloth Objectボタンを押して、ビューポートでオブジェクトを選んで、Enterを押します。 f:id:ushiostarfish:20180909194451p:plain

この操作で自動的にシミュレーション用のノードが構成されます。（ここの構造あんまり慣れておらず、理解が浅いです。すみませんすると、フレームを進めるとすでに自由落下をはじめます。 f:id:ushiostarfish:20180909194543p:plain

適当なオブジェクトを配置します。ポリゴンになってないとシミュレーションがうまくいきませんでした。 f:id:ushiostarfish:20180909194821p:plain

今度はCloth Objectボタンと同様に、Static Objectボタンを押して選択すると、自動的にシミュレーションノードに組み込まれます。 f:id:ushiostarfish:20180909195023p:plain

あとはオブジェクトサイズとか、物理パラメータを微調整するなどしつつ、シミュレーションすれば、 f:id:ushiostarfish:20180909195625g:plain

シミュレーションのポリゴンが荒い場合は、Subdivideノードを挟むだけで綺麗になります。 f:id:ushiostarfish:20180909195800p:plain

床

床がちょっとだけ寂しかったので、模様をつけることにしました。まずはボックスを用意して、 f:id:ushiostarfish:20180909200230p:plain

グリッドをラインに変換したあと、 f:id:ushiostarfish:20180909200303p:plain

ワイヤーメッシュ化して、 f:id:ushiostarfish:20180909200414p:plain

Booleanで表面を削ってしまいます。 f:id:ushiostarfish:20180909200511p:plain

これだけです。結構プログラミングのアイディアを簡単に組み込んでいけるHoudiniは、楽しいものです。興味の湧いた方はまずはApprentice版をダウンロード！

www.sidefx.com

部屋から見えた夕日

f:id:ushiostarfish:20180908193202j:plain

すごかったです。そして来年の合宿も楽しみです。運営の皆様、大変ありがとうございました！

2018-07-15

エネルギー保存Microfacet BRDF

レイトレーシング

この記事はレイトレ合宿6アドベントカレンダー第3週目の記事です。

概要

前回 Microfacet入門（１） - ushiostarfish’s diary では、多重拡散を考慮しないナイーヴなマイクロファセットモデルではエネルギーが完全には保存せず、一部が失われてしまう問題について触れました。そこで今回はその問題への対処として、ややアドホックではありますが、とてもシンプルで軽量な解決方法を提案している、 Csaba Kelemen and László Szirmay-Kalos, "A Microfacet Based Coupled Specular-Matte BRDF Model with Importance Sampling" (以降 [Kelemen 2001] のアイディアに触れてみようと思います。

[Kelemen 2001] のアプローチ

[Kelemen 2001] のアプローチは一言でいうと、単一拡散モデルで失われたエネルギーを、ランバート反射のような均質な拡散反射で補填する、というものです。 [Kelemen 2001] では鏡面反射成分をよくある単一拡散マイクロファセットモデルの以下の形式を用いて記述します。

$\displaystyle { f_{ r,spec }\left( \omega _{ i },\omega _{ o } \right) =\frac { F\left( \lambda ,\omega _{ h }\cdot \omega _{ i } \right) G_{ 2 }\left( \omega _{ h },\omega _{ i },\omega _{ o } \right) D\left( \omega _{ h } \right) }{ 4\left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } }$

※論文中では $D\left( \omega _{ h } \right)$ の代わりに $P_{ H }\left( \omega _{ h } \right)$ が使われておりますが、同じです。

Fはフレネル項であり、波長依存性を明示的にλを引数に取ることで主張しつつ、Gはシャドウイング・マスキング関数で、論文中はV-Cavityが用いられています。Dは法線分布関数で、論文中はBeckmann分布が用いられています。
自分も今回はそれにならってV-Cavity, Beckmannを使っていくことにします。（この記事の中ではその詳細には立ち入らず、この部分は後日別記事にするかもしれません）ただし、論文中のコアアイディアとしては、各関数に何を用いるのかはさほど重要なポイントではありません。

当然ながら、これはエネルギーを完全には保存しません。

$\displaystyle { \int _{ \Omega _{ o } }^{ }{ f_{ r,spec }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ o } } d\omega _{ o } } \le 1\forall \omega _{ i } }$

そこで、失われたエネルギーを補うマット成分の項を追加して、

$\displaystyle { f_{ r }\left( \omega _{ i },\omega _{ o } \right) =f_{ r,spec }\left( \omega _{ i },\omega _{ o } \right) +f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) \\ \int _{ \Omega _{ o } }^{ }{ f_{ r }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ o } } d\omega _{ o } } =1\forall \omega _{ i } }$

これならエネルギーが保存されます。これは強引に解釈するとすれば、多重拡散した結果指向性を失い、マット成分として放出された、というふうに言えなくもないかもしれません。

スペキュラ反射能

実際のところ、エネルギーを補うためには、そもそもどの程度エネルギーが失われているのかを測る必要があります。そこで全体のエネルギー反射率を、 $\theta '$ から入射するときのスペキュラ反射能として、以下のように定義します。

$\displaystyle { a_{ spec }\left( \theta ' \right) =a_{ spec }\left( \vec { L } \right) =\int _{ \Omega _{ o } }^{ }{ f_{ r,spec }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ o } } d\omega _{ o } } }$

スペキュラ反射能は、単位放射照度あたりの、出射の放射輝度を全部かき集めたもの(=放射発散度)、と解釈できます。BRDFの単位は1/srですので、積分した値は無次元数であり、エネルギーの保存率と考えても良さそうです。また、きちんと相反するBRDFを考えているなら、反射能についても出射と入射どちらを考えても同じ関数になります。指向性アルベドとも呼ばれるそうです。

$\displaystyle { a_{ spec }\left( \theta ' \right) =a_{ spec }\left( \vec { L } \right) =a_{ spec }\left( \vec { V } \right) =a_{ spec }\left( \theta \right) }$

マット項

理想的には、多重拡散項がClosed-formに求まるのがベストですが、現状は難しく、Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-Scattering Microfacet BSDFs with the Smith Model" ですら、確率的な評価にならざるを得ず、さらに理論はヘビーでとても難しいです。[Kelemen 2001] では、一昔前の論文ではありますが、もっとシンプルに以下のようにマット成分を記述することにしてます。

$\displaystyle { f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) =k\left( \lambda \right) \cdot s\cdot r\left( \theta ' \right) \cdot r\left( \theta \right) }$

kは適当な吸収係数であり、rはそれぞれ入射・出射に依存する関数を個別に定義し、sは正規化項として後ほど明らかにします。 kにはλが引数になっているのは、ここに適当な色をつけたりなどが想定されています。

ここでこのマット項の反射能を考えてみると、スペキュラ反射能と同様に、

$\displaystyle { a_{ matte }\left( \theta ' \right) =a_{ matte }\left( \vec { L } \right) =\int _{ \Omega _{ o } }^{ }{ f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ o } } d\omega _{ o } } }$

となります。ここで積分を重積分に展開して、 $\theta '$ に依存しない項を外に出すと、

$\displaystyle { a_{ matte }\left( \theta ' \right) =\int _{ \Omega _{ o } }^{ }{ f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ o } } d\omega _{ o } } \\ =\int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ k\left( \lambda \right) \cdot s\cdot r\left( \theta ' \right) \cdot r\left( \theta \right) \cos { \theta } \sin { \theta } d\theta } d\phi } \\ =k\left( \lambda \right) \cdot s\cdot 2\pi \cdot r\left( \theta ' \right) \int _{ 0 }^{ \frac { \pi }{ 2 } }{ r\left( \theta \right) \cos { \theta } \sin { \theta } d\theta } }$

この式をよく見てみると、 $a_{ matte }\left( \theta ' \right)$ は、 $r\left( \theta ' \right)$ に比例しており、他の項は定数であることがわかります。ここで $a_{ matte }\left( \theta ' \right)$ は別の観点、スペキュラ反射能のロスがマット反射能だという仮定からみると、

$\displaystyle { a_{ matte }\left( \theta ' \right) =1-a_{ spec }\left( \theta ' \right) }$

もまた同時に言え、 $a_{ matte }\left( \theta ' \right)$ は、 $1-a_{ spec }\left( \theta ' \right)$ に比例しており、さらにこれは入射と出射の立場を入れ替えても同じことが言えるわけなのでもはや、

$\displaystyle { r\left( \theta ' \right) =1-a_{ spec }\left( \theta ' \right) \\ r\left( \theta \right) =1-a_{ spec }\left( \theta \right) }$

としてしまっても差し支えないのではないでしょうか。すると、

$\displaystyle { f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) =k\left( \lambda \right) \cdot s\cdot r\left( \theta ' \right) \cdot r\left( \theta \right) \\ f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) =k\left( \lambda \right) \cdot s\cdot \left( 1-a_{ spec }\left( \theta ' \right) \right) \cdot \left( 1-a_{ spec }\left( \theta \right) \right) }$

となりました。ここで正規化項が何になるか考えるために、

$\displaystyle { a_{ matte }\left( \theta ' \right) =\int _{ \Omega _{ o } }^{ }{ f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ o } } d\omega _{ o } } }$

から初めて、

$\displaystyle { 1-a_{ spec }\left( \theta ' \right) =\int _{ \Omega _{ o } }^{ }{ f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ o } } d\omega _{ o } } \\ 1-a_{ spec }\left( \theta ' \right) =\int _{ \Omega _{ o } }^{ }{ s\cdot \left( 1-a_{ spec }\left( \theta ' \right) \right) \left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta _{ o } } d\omega _{ o } } \\ \left( 1-a_{ spec }\left( \theta ' \right) \right) =s\cdot \left( 1-a_{ spec }\left( \theta ' \right) \right) \int _{ \Omega _{ o } }^{ }{ \left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta _{ o } } d\omega _{ o } } \\ 1=s\int _{ \Omega _{ o } }^{ }{ \left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta _{ o } } d\omega _{ o } } \\ s=\frac { 1 }{ \int _{ \Omega _{ o } }^{ }{ \left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta _{ o } } d\omega _{ o } } } \\ s=\frac { 1 }{ \int _{ \Omega _{ o } }^{ }{ \cos { \theta _{ o } } d\omega _{ o } } -\int _{ \Omega _{ o } }^{ }{ a_{ spec }\left( \theta \right) \cos { \theta _{ o } } d\omega _{ o } } } \\ s=\frac { 1 }{ \pi -\int _{ \Omega _{ o } }^{ }{ a_{ spec }\left( \theta \right) \cos { \theta _{ o } } d\omega _{ o } } } \\ s=\frac { 1 }{ \pi -\pi \frac { 1 }{ \pi } \int _{ \Omega _{ o } }^{ }{ a_{ spec }\left( \theta \right) \cos { \theta _{ o } } d\omega _{ o } } } }$

ここで、

$\displaystyle { a_{ spec }^{ avg }=\frac { 1 }{ \pi } \int _{ \Omega }^{ }{ a_{ spec }\left( \theta \right) \cos { \theta } d\omega } }$

と平均のアルベドを定義すると、

$\displaystyle { s=\frac { 1 }{ \pi -\pi a_{ spec }^{ avg } } \\ s=\frac { 1 }{ \pi \left( 1-a_{ spec }^{ avg } \right) } }$

とスッキリと記述できてしまいました。これをsの代わりに使うと、

$\displaystyle { f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) =k\left( \lambda \right) \cdot \frac { \left( 1-a_{ spec }\left( \theta ' \right) \right) \cdot \left( 1-a_{ spec }\left( \theta \right) \right) }{ \pi \left( 1-a_{ spec }^{ avg } \right) } }$

とマット項が定まりました。なんともシンプルな結果であり、かつ相反性を満たし、エネルギーを完全に保存します
ただ残念なことは、 $a_{ spec }^{ avg }$ も $a_{ spec }\left( \theta \right)$ も解析的に求めることができず、事前計算でテーブルに格納しなければならない点です。等方的なら、前者は２次元テーブル（α, θ）、後者は１次元テーブル（α）で済みます。

フレネル項

論文中では、 $a_{ spec }\left( \theta \right)$ を求めるとき、スペキュラ項に誘導体フレネルを含んでいます。この実装では、以下のような見た目になります。

f:id:ushiostarfish:20180624201701p:plain

※Figure 7, [Kelemen 2001]

多層マテリアルのような見た目です。これはある意味当たり前で、誘導体の中に潜り込んだ分のエネルギーを拡散項として放出しているからです。

これはこれで綺麗だと思う反面、物理的な意味に乏しいという欠点はあります。ただこれはかならずしも誘導体フレネルでやらねければならないわけではなく、導体マテリアルのエネルギー補填として使うことを考え、フレネル項を省いたスペキュラ項で $a_{ spec }\left( \theta \right)$ を求めておいて使うことが可能です。こちらも物理的意味には乏しいものの、Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-Scattering Microfacet BSDFs with the Smith Model" をGround Truthとした近似手法が一部で試みがあるようで、Self Shadow, "A Multi-Faceted Exploration (Part 1)" や PataBlog, "Multiple-Scattering BRDF" で確認することができます。以降は導体マテリアルに使うことをメインよりにすすめていこうと思います。

$a_{ spec }^{ avg }$ と $a_{ spec }\left( \theta \right)$ のベイク

[Kelemen 2001] の手法は、アイディアと式はとてもシンプルな反面、テーブルへの格納とサンプリングを余儀なくされるため、実装側はやや面倒です。ここでは計算結果を Cereal を使ってデータをまるっとシリアライズすることにします。また、テーブルを引くとときに、補間処理が必要なので、とりあえずwikipediaからコピペしてきたbicubic補間を使うことにしました。汎用的に使えるようにテンプレートにしつつ、以下のようにしました。

これを使って、まずは $a_{ spec }\left( \theta \right)$ です。

保存は以下のようにします

$a_{ spec }\left( \theta \right)$ は、なんだったかというと、

でした。したがって、V-Cavity, Beckmann を使ってベイクするコードは、

のようにしました。導体と誘導体の２種類をここではベイクする想定です。積分方法は、 $a_{ spec }\left( \theta \right)$ は単純にモンテカルロ法でやりました。合成シンプソンとかでもいいのかな？とも思ったのですが、αが小さいとき、誤差が大きくなる問題もあったのと、効率的な重点サンプリングが存在しているというのが大きいです。ベイクした結果を可視化するために、exrで保存しておくと、デバッグに便利でした。一部 openframeworks のコードが混在してしまっていますが、やっていることは伝わるのではないでしょうか

ベイクするサイズはどのくらいが良いのか？というのを決めなくてはなりませんが、実際 $a_{ spec }^{ avg }$ も $a_{ spec }\left( \theta \right)$ もかなり緩やかでなめらかな形をしているため、それほど大きな解像度は必要なさそうです。imageworksのスライドでは、32x32を使っているようですが、自分は今回は大きめの64x64にしました。

実際どんなかんじになるのかというと、導体のフレネルのケースでは例えば以下のようになります（画像は拡大しています）。もちろん使ったDやG（もし誘導体ならFも）にも影響されるでしょう

f:id:ushiostarfish:20180701164033p:plain

一番右下の暗いところは、0.7くらいの数値になっていました。粗さαが高くて、入射（出射）角度が0に近い部分は多重拡散のエネルギーロスが激しいことがわかります。

次に $a_{ spec }\left( \theta \right)$ ですが、これは、

$\displaystyle { a_{ spec }^{ avg }=\frac { 1 }{ \pi } \int _{ \Omega }^{ }{ a_{ spec }\left( \theta \right) \cos { \theta } d\omega } }$

でした。しかし実際のところ、

$\displaystyle { a_{ spec }^{ avg }=\frac { 1 }{ \pi } \int _{ \Omega }^{ }{ a_{ spec }\left( \theta \right) \cos { \theta } d\omega } \\ =\frac { 1 }{ \pi } \int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ a_{ spec }\left( \theta \right) \cos { \theta } \sin { \theta } d\theta } d\phi } \\ =\frac { 1 }{ \pi } 2\pi \int _{ 0 }^{ \frac { \pi }{ 2 } }{ a_{ spec }\left( \theta \right) \cos { \theta } \sin { \theta } d\theta } \\ =2\int _{ 0 }^{ \frac { \pi }{ 2 } }{ a_{ spec }\left( \theta \right) \cos { \theta } \sin { \theta } d\theta } }$

と一次元の積分に落とすことができるため、こちらを使うのが良いでしょう。こちらは以下のようにコードにしました。

ベイクのほうは、合成シンプソンを使って、

ベイクは、

のようにしました。これは例えば導体の場合、

f:id:ushiostarfish:20180701154436p:plain

のような結果になりました。

[Kelemen 2001] の近似について

[Kelemen 2001] の2.1.1. Simplification of the geometric term ～あたりで、G項の一部を簡略化することで、BRDFやその重点サンプリングの式を軽量化・テーブル化できることを提案しています。しかしながら、その結果は視覚誤差もあり、後により良い重点サンプリングが提案されているため、この部分の有用度は低いと思われます。導出も別段すごく面白いというわけでもなかったので、ここではこれは使わないことにしました。

実装

あとはストレートに、

をベーシックなマイクロファセットのBRDFに足せば良いです。実装は例えば、

glm::dvec3 brdf_diff = kLambda
    * (1.0 - CoupledBRDFConductor::specularAlbedo().sample(alpha, cos_term_wo))
    * (1.0 - CoupledBRDFConductor::specularAlbedo().sample(alpha, cos_term_wi))
    / (glm::pi<double>() * (1.0 - specularAlbedo));

のようになるでしょう。

重点サンプリング

次に拡散項の重点サンプリングについてです。同時に考えると難しいので、やはりここは $f_{ r,spec }$ と $f_{ r,matte }$ を分離して考えます。出射放射輝度のそれぞれの割合は、

$\displaystyle { 1=\int _{ \Omega _{ i } }^{ }{ \left\{ f_{ r,spec }\left( \omega _{ i },\omega _{ o } \right) +f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) \right\} \cos { \theta _{ i } } d\omega _{ i } } \\ =\int _{ \Omega _{ i } }^{ }{ f_{ r,spec }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ i } } d\omega _{ i } } +\int _{ \Omega _{ i } }^{ }{ f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ i } } d\omega _{ i } } \\ =a_{ spec }\left( \theta \right) +a_{ matte }\left( \theta \right) \\ =a_{ spec }\left( \theta \right) +\left( 1-a_{ spec }\left( \theta \right) \right) }$

となるので、このエネルギー比率をそれぞれをサンプルする確率にすれば良さそうです。ただこれはあくまで吸収係数 $k \left( \lambda \right)$ や、導体想定で $a_{ spec }\left( \theta \right)$ のベイク時にフレネル項が含まれていない場合は実際の $f_{ r,spec }$ には追加でフレネル項が入るわけです。なのでここはちょっと場合分けが必要のように思います。

ベイクするときに誘導体フレネルを含んだ場合

この場合、吸収係数 $k \left( \lambda \right)$ は任意の色をつけるために使う用途が想定されます。そして、したがって例えば以下のような比率でサンプリングを組み合わせる方法があります。

$\displaystyle { a_{ spec }\left( \theta \right) :\widetilde { k } \left( 1-a_{ spec }\left( \theta \right) \right) }$

ここで $\widetilde { k }$ は例えば波長それぞれの平均が使えるでしょう。ただそれは最適かというとそうでもなく、平均の代わりにXYZ色空間へ変換して輝度が集約されたY成分を使ったりする実装もありなのではないでしょうか。まあ $\widetilde { k }$ の実装方法は一旦おいておいて、実際の確率は、

$\displaystyle { P_{ spec }=\frac { a_{ spec }\left( \theta \right) }{ a_{ spec }\left( \theta \right) +\widetilde { k } \left( 1-a_{ spec }\left( \theta \right) \right) } \\ P_{ matte }=\frac { \widetilde { k } \left( 1-a_{ spec }\left( \theta \right) \right) }{ a_{ spec }\left( \theta \right) +\widetilde { k } \left( 1-a_{ spec }\left( \theta \right) \right) } =1-P_{ spec } }$

となります。

導体想定の、ベイクするときにフレネル項を含まなかった場合

$f_{ r,spec }$ にはベイク時には考慮していないフレネル項を追加してレンダリングします。しかし後述しますが、吸収係数 $k \left( \lambda \right)$ を多重拡散時の色を近似する項として使用する予定です。なので結局どちらの項にも同一ではないもののフレネル項を使います。なのでここでは簡単のため吸収係数 $k \left( \lambda \right)$ を気にしないことにします。よって確率は、

$\displaystyle { P_{ spec }=a_{ spec }\left( \theta \right) \\ P_{ matte }=1-a_{ spec }\left( \theta \right) }$

を使うことにします。

組み合わせる場合の確率密度

組み合わせる、とはどういうことかというと、 $P_{ spec }$ の確率で $PDF_{ spec }$ (確率密度) のサンプリングが起こり、 $P_{ matte}$ の確率で $PDF_{ matte}$ (確率密度)のサンプリング起こるようにします。したがってその場合の確率密度は、

$\displaystyle { P_{ spec }\times PDF_{ spec }+P_{ matte }\times PDF_{ matte } }$

とすれば良いことがわかります。

$f_{ r,matte }$ の重点サンプリング

$f_{ r,matte }$ は、以下の式でした。

ここで $\omega_i$ をサンプリングすることを考えた場合、 $\omega_i$ に依存しない項を定数項として全部まとめ上げると、

$\displaystyle { f_{ r,matte }\left( \omega _{ i },\omega _{ o } \right) =T\left( 1-a_{ spec }\left( \theta ' \right) \right) =T\left( 1-a_{ spec }\left( \theta \right) \right) }$

となり、LTEとしては、

$\displaystyle { L_{ o }=\int _{ \Omega _{ i } }^{ }{ L_{ i }T\left( 1-a_{ spec }\left( \theta _{ i } \right) \right) \cos { \theta _{ i } } d\omega _{ i } } }$

とこのようになるので、BRDFのサンプリングとしては、

$\displaystyle { \left( 1-a_{ spec }\left( \theta _{ i } \right) \right) \cos { \theta _{ i } } }$

に比例するように $\omega_i$ がサンプリングされるのが良いと思われます。ここでもし完璧な確率密度関数 $p_{ exact }\left( \omega \right)$ が手に入ったとしたら、以下のような形になるでしょう。

$\displaystyle { p_{ exact }\left( \omega \right) =T\left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta } \\ 1=\int _{ \omega }^{ }{ T\left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta } d\omega } }$

T は適切に求められた正規化定数とします。これを $\theta$ の積分に持っていくと、

$\displaystyle { 1=\int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ T\left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta } \sin { \theta } d\theta } d\phi } \\ 1=\int _{ 0 }^{ 2\pi }{ d\phi \int _{ 0 }^{ \frac { \pi }{ 2 } }{ T\left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta } \sin { \theta } d\theta } } \\ 1=2\pi \int _{ 0 }^{ \frac { \pi }{ 2 } }{ T\left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta } \sin { \theta } d\theta } \\ 1=\int _{ 0 }^{ \frac { \pi }{ 2 } }{ 2\pi T\left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta } \sin { \theta } d\theta } }$

なので実際には、

$\displaystyle { \left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta } \sin { \theta } }$

に比例するように $\theta$ をサンプリングするのが良いことがわかります。

[Kelemen 2001] ではこれを、解析的ではないものの事前計算テーブルを使った逆関数法が紹介されています。しかしどうにもこの論文では $\sin \theta$ を無視しているようなのと、個人的にはサンプリングについてはunbiasedなものを使いたいと考えたのでこの部分はちょっと変えることにしました。

まずは単純に $\theta_{ i }$ の範囲を均等にn分割して、

f:id:ushiostarfish:20180704001859p:plain

そこの代表点を $\left( 1-a_{ spec }\left( \theta \right) \right) \cos { \theta } \sin { \theta }$ で評価します。あとはその値に比例して範囲が選ばれるようにします。次にその範囲内均一に $\theta$ をサンプリングします。あとは $\phi$ もまた均一にサンプリングすれば、半球に欲しかった性質を持つサンプルを生成できます。

しかし残念ながらこれだけではだめで、我々は実際の確率密度関数が必要です。なのでこの場合どんな確率密度になるのか考えてみます。

まずn分割した区間個別は、

$\displaystyle { b-a=\frac { \frac { \pi }{ 2 } }{ n } =\frac { \pi }{ 2n } }$

であり、それぞれの範囲の中では均一にサンプリングすることにしたため、個別の範囲の確率密度関数 $p_{ x_{ i } }$ と表記すると、

$\displaystyle { p_{ x_{ i } }=\frac { 2n }{ \pi } }$

であると言えます。そして実際のところある特定の一箇所が選ばれる確率密度は、その範囲がまず選ばれていなければいけません。なので $\theta$ の確率密度関数 $p\left( \theta \right)$ は、離散的な確率との積になるはずです。

$\displaystyle { p\left( \theta \right) =p_{ x_{ i } }p_{ discrete }\left( x_{ i } \right) \\ p\left( \theta \right) =\frac { 2n }{ \pi } p_{ discrete }\left( x_{ i } \right) }$

例えば n=1、つまり完全に均一にサンプリングする場合、

$\displaystyle { p\left( \theta \right) =\frac { 2 }{ \pi } }$

と確かに辻褄が合っています。また他に簡単にテストするとして、積分して1になるか確かめてみます。

$\displaystyle { X=\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \frac { 2n }{ \pi } p_{ discrete }\left( \theta \right) d\theta } \\ \frac { \pi }{ 2n } X=\int _{ 0 }^{ \frac { \pi }{ 2 } }{ p_{ discrete }\left( \theta \right) d\theta } }$

ここで $p_{ discrete }\left( \theta \right)$ はきれいな短冊形の関数なので、

$\displaystyle { \frac { \pi }{ 2n } X=\sum _{ i=1 }^{ n }{ \frac { b-a }{ n } p_{ discrete }\left( x_{ i } \right) } \\ \frac { \pi }{ 2n } X=\sum _{ i=1 }^{ n }{ \frac { \frac { \pi }{ 2 } -0 }{ n } p_{ discrete }\left( x_{ i } \right) } \\ \frac { \pi }{ 2n } X=\sum _{ i=1 }^{ n }{ \frac { \pi }{ 2n } p_{ discrete }\left( x_{ i } \right) } \\ X=\sum _{ i=1 }^{ n }{ p_{ discrete }\left( x_{ i } \right) } =1 }$

と確かに1になりました。一方 $\phi$ の確率密度関数はどうなるかというと、こちらも均一にサンプリングするため、

$\displaystyle { p\left( \phi \right) =\frac { 1 }{ 2\pi } }$

になります。これを２次元のサンプリングで捉えると、

$\displaystyle { 1=\int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ p\left( \theta \right) p\left( \phi \right) d\theta } d\phi } \\ 1=\int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ \frac { p\left( \theta \right) p\left( \phi \right) }{ \sin { \theta } } \sin { \theta } d\theta } d\phi } \\ 1=\int _{ \omega }^{ }{ \frac { p\left( \theta \right) p\left( \phi \right) }{ \sin { \theta } } d\omega } }$

したがって、立体角での確率密度関数は、

$\displaystyle { p\left( \theta \right) =\frac { 2n }{ \pi } p_{ discrete }\left( \theta \right) \\ p\left( \phi \right) =\frac { 1 }{ 2\pi } \\ p\left( \omega \right) =\frac { p\left( \theta \right) p\left( \phi \right) }{ \sin { \theta } } \\ p\left( \omega \right) =\frac { n }{ { \pi }^{ 2 }\sin { \theta } } p_{ discrete }\left( \theta \right) }$

となります。

実装例

まずは任意の個数の、数値に比例する離散的なサンプルを生成できるクラスを以下のようにしました。

そして実際にサンプルを生成するところは以下のようにしました。テーブルサイズは32x128ですが、これにあまり根拠はありません。もうちょっと小さくても良いかもしれません。

これらを使って、あとはサンプルと確率密度は、以下のようにしました。

これで重点サンプリングの実装は完了です。この構築アプローチは積分を解く必要がなく、テーブルサイズも小さいため、わざわざベイクする必要はないと判断し、レンダラー起動時に計算することにしました。

White Furnace Test

完全にエネルギーを保存するBRDFでは、最初に触れたとおり、

$\displaystyle { \int _{ \Omega _{ o } }^{ }{ f_{ r }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ o } } d\omega _{ o } } =1\quad \forall \omega _{ i } }$

となるべきです。これはiとoを入れ替えても

$\displaystyle { \int _{ \Omega _{ i } }^{ }{ f_{ r }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ i } } d\omega _{ i } } =1\quad \forall \omega _{ o } }$

これは、LTEにおいて、 $L_{ e }=1$ かつ $L_{ i }=1$ のケースであり、

$\displaystyle { L_{ o }=L_{ e }+\int _{ \Omega _{ i } }^{ }{ L_{ i }f_{ r }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ i } } d\omega _{ i } } \\ =\int _{ \Omega _{ i } }^{ }{ f_{ r }\left( \omega _{ i },\omega _{ o } \right) \cos { \theta _{ i } } d\omega _{ i } } }$

これは、"周囲からの放射輝度がすべて1の場合、出射放射輝度は常に1であるべきだ" という解釈ができます。これをテストする手法を "White Furnace Test" と呼びます。これは単にコードベースの単体テストとしても有効ですが、例えばテストしたいマテリアルを適用した球体を、出射放射輝度が全方位で1、反射0の理想拡散光源で囲んで、レンダリングする。という方法があります。（反射0でなくても、直接照明だけに計算を限定しても良いでしょう）球体自身はいろんな出射角度を持つものの、やはりその出射放射輝度は1であるはずで、球体の後ろ側の背景もやっぱり1になるべき、つまり真っ白な画像が出てくるべきだ、というわけです。

実際、例えば通常の単一拡散マイクロファセット導体マテリアルのフレネルがないケースにおいて、α=1としてこのテストを実施すると、

f:id:ushiostarfish:20180701165833p:plain

のようになり、中心付近の数値が0.7くらいになります。これは $a_{ spec }\left( \theta \right)$ のベイクと結果が一致しています。本質的に同じ方程式を解いているからですね。

一方で完全にエネルギー保存するようなケース、例えば、 Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-Scattering Microfacet BSDFs with the Smith Model" の場合を試してみます。これは、tutorial implementation (documentation, code and unit tests)にソースコードがあるので、ちょっとこれを借りることにします。

MicrosurfaceConductorクラスのevalを呼ぶと f * cosθoが、確率的な評価ではありますが、BRDFを評価することができます。重点サンプリングも提供してくれていますが、あとで使いたいフレネルを含ませるやり方がわからなかったため、ここではevalを使いつつ、重点サンプリングは通常の単一拡散のものを使いつつ、uniformなサンプリングを織り交ぜることにしました。

glm::dvec3 sample(PeseudoRandom *random, const glm::dvec3 &wo) const override {
    glm::dvec3 wi;
    double singleScattering = 0.8;
    if (random->uniform() < singleScattering) {
        wi = VCavityBeckmannVisibleNormalSampler::sample(random, alpha, wo, Ng);
    }
    else {
        wi = UniformHemisphereSampler::sample(random, Ng);
    }
    return wi;
}
double pdf(const glm::dvec3 &wo, const glm::dvec3 &sampled_wi) const override {
    double singleScattering = 0.8;
    double pdf_omega =
        0.8 * VCavityBeckmannVisibleNormalSampler::pdf(sampled_wi, alpha, wo, Ng)
        +
        (1.0 - singleScattering) * UniformHemisphereSampler::pdf(sampled_wi, Ng);
    return pdf_omega;
}

これを使ってWhite Furnace Testを実行すると、

f:id:ushiostarfish:20180701171303p:plain

多少の分散こそありますが、見事に成功しています。では多重拡散の代わりに、新しく作った、エネルギー補填項を持つCouple BRDFはどうでしょうか？

f:id:ushiostarfish:20180701171748p:plain

素晴らしい、確かにWhite Furnace Testに成功しています。

"Multiple-Scattering Microfacet BSDFs with the Smith Model" との比較

もうちょっと複雑なシーンではCouple BRDFはどのような見た目になるのかテストしてみましょう。また、同時に"Multiple-Scattering Microfacet BSDFs with the Smith Model"はclosed-formではないものの、多重拡散の"Ground Truth" と言っても差し支えないと思いますので、それとの比較を積極的にやっていくことにします。

シーンはこんなかんじです。モデルは、McGuire Computer Graphics Archive のMori Knobをお借りしました。

f:id:ushiostarfish:20180701172718p:plain

rouphnessについては、 $\alpha = \left( rouphness \right) ^2$ としました。

ここでまずはフレネル項を除いたケースを考えてみます。

まずは通常の単一拡散の場合です。 f:id:ushiostarfish:20180708003229p:plain

確かにラフネス値が高いとエネルギーが失われた結果、不必要に暗くなっているのがわかります。

一方でCouple BRDFはどうなるかというと、 f:id:ushiostarfish:20180708003236p:plain

"Multiple-Scattering Microfacet BSDFs with the Smith Model" の場合はどうなるかというと、 f:id:ushiostarfish:20180708003252p:plain

物理的な意味には乏しいにもかかわらず、かなり見た目が近いです！では今度はフレネル項を追加することを考えます。

"Multiple-Scattering Microfacet BSDFs with the Smith Model" の場合、Supplemental Material: Implementationを読むと、以下のように追加すれば良さそうです。

float MicrosurfaceConductor::evalPhaseFunction(const vec3& wi, const vec3& wo) const
{
    // half vector 
    const vec3 wh = normalize(wi+wo);
    if(wh.z < 0.0f)
        return 0.0f;
    
#if USE_FRESNEL
    // Fresnel
    const float F = fresnel_unpolarized(n, k, glm::dot(wi, wh));

    // value
    const float value = 0.25f * F * m_microsurfaceslope->D_wi(wi, wh) / dot(wi, wh);
#else 
    // value
    const float value = 0.25f * m_microsurfaceslope->D_wi(wi, wh) / dot(wi, wh);
#endif
    return value;
}

ここでフレネル項は、Ole Gulbrandsen Framestore, "Artist Friendly Metallic Fresnel" でも使われている、複素屈折率 $\eta = n+ik$ をパラメータにもつフレネル反射の近似式（元はPBRT v2で、v3では見当たらない・・・？）である、

$\displaystyle { r_{ \bot }\left( n,k,\theta \right) =\frac { n^{ 2 }+k^{ 2 }-2\eta \cos \theta +\cos ^{ 2 }{ \theta } }{ n^{ 2 }+k^{ 2 }+2\eta \cos \theta +\cos ^{ 2 }{ \theta } } \\ r_{ \parallel }\left( n,k,\theta \right) =\frac { \left( n^{ 2 }+k^{ 2 } \right) \cos ^{ 2 }{ \theta } -2n\cos \theta +1 }{ \left( n^{ 2 }+k^{ 2 } \right) \cos ^{ 2 }{ \theta } +2n\cos \theta +1 } \\ F\left( n,k,\theta \right) =\frac { r_{ \bot }\left( n,k,\theta \right) +r_{ \parallel }\left( n,k,\theta \right) }{ 2 } }$

を使うことにしました。今回はナイーヴなRGBレンダラーを想定して、代表的な波長を

color	wavelength
R	650nm
G	550nm
B	450nm

としました。あまり強い根拠はなく、Complex Fresnel shader - OSL Shaders - Chaos Group Help のマネをしただけです。

例えば金の場合は、

color	n	k
R	0.15557	3.6024
G	0.42415	2.4721
B	1.3821	1.9155

※ Refractive index of Au (Gold) - Johnson より

を使って、これを元に "Multiple-Scattering Microfacet BSDFs with the Smith Model" でレンダリングすると以下のようになりました。

f:id:ushiostarfish:20180708003448p:plain

綺麗です。Coupled でも試してみます。しかしこの場合は一つ問題があり、

の

$k\left( \lambda \right)$ をどうするのか？という点です。普通に考えると多重拡散項もフレネル項の影響を受けるはずです。しかし一旦忘れて $k\left( \lambda \right)$ を1でレンダリングしてみます。すると、

f:id:ushiostarfish:20180708003509p:plain

うーん、近いことは近いです。しかしαが1に近くなるにつれて白くなりすぎています。もうちょっとなんとかならないでしょうか？

多重拡散項の近似

ここの多重拡散項をより近づけるための手法として、今回は siggraph 2017のimageworksの資料および、A Multi-Faceted Exploration (Part 2) - Self Shadow を参考にしてみることにします。

まずある一回の衝突では、全体のエネルギーを1としたとき、平均的に見て $a_{ spec }^{ avg }$ が単一拡散、 $1-a_{ spec }^{ avg }$ が多重拡散として衝突を続けると考えられます。ただ多重拡散項はまた次の衝突で、 $a_{ spec }^{ avg }$ と $1-a_{ spec }^{ avg }$ の割合で分断されます。このプロセスが再帰的に繰り返されると考えられます。そして衝突した分だけフレネル項の影響を受けるでしょう。ただフレネル項も多重拡散分は角度が不明であるため、cos重みづけ平均をここでのフレネル項とします。

$\displaystyle { F_{ avg }\left( \eta ,k \right) =\int _{ \Omega }^{ }{ \frac { 1 }{ \pi } F\left( \eta ,k,\cos { \theta } \right) \cos { \theta } d\omega } }$

実際これは、

$\displaystyle { F_{ avg }\left( \eta ,k \right) =\int _{ \Omega }^{ }{ \frac { 1 }{ \pi } F\left( \eta ,k,\cos { \theta } \right) \cos { \theta } d\omega } \\ =\int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ \frac { 1 }{ \pi } F\left( \eta ,k,\cos { \theta } \right) \cos { \theta } \sin { \theta } d\theta } d\phi } \\ =2\pi \int _{ 0 }^{ \frac { \pi }{ 2 } }{ \frac { 1 }{ \pi } F\left( \eta ,k,\cos { \theta } \right) \cos { \theta } \sin { \theta } d\theta } \\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ 2F\left( \eta ,k,\cos { \theta } \right) \cos { \theta } \sin { \theta } d\theta } }$

と単純化でき、さらに

$\displaystyle { \mu =\cos { \theta } \\ \frac { d\mu }{ d\theta } =-\sin { \theta } \\ -d\mu =\sin { \theta } d\theta }$

と変数変換すると、

$\displaystyle { =-\int _{ \cos { 0 } }^{ \cos { \frac { \pi }{ 2 } } }{ 2F\left( \eta ,k,d \right) \mu d\mu } \\ =-\int _{ 1 }^{ 0 }{ 2F\left( \eta ,k,d \right) \mu d\mu } \\ =2\int _{ 0 }^{ 1 }{ F\left( \eta ,k,d \right) \mu d\mu } }$

とさらに簡単になり、なめらかでゆるやかな関数のため、合成シンプソンなどで少ない評価点でも近似できます。

以上をふまえ、 $E=a_{ spec }^{ avg }$ 、フレネルを $F$ として図にしてみます。

f:id:ushiostarfish:20180701180926p:plain

これを式にすると、

$\displaystyle { FE+F\left( 1-E \right) +{ \left\{ F\left( 1-E \right) \right\} }^{ 2 }+{ \left\{ F\left( 1-E \right) \right\} }^{ 3 }+...\\ =FE\sum _{ k=0 }^{ \infty }{ { \left\{ F\left( 1-E \right) \right\} }^{ k } } }$

となり、これは等比数列の和として解くことができるので、

$\displaystyle { a=FE\\ r=F\left( 1-E \right) \\ a+ar+a{ r }^{ 2 }+...a{ r }^{ n-1 }={ \frac { a\left( 1-r^{ n } \right) }{ 1-r } }\\ =\frac { FE\left( 1-{ { \left\{ F\left( 1-E \right) \right\} }^{ \infty } } \right) }{ 1-F\left( 1-E \right) } =\frac { FE }{ 1-F\left( 1-E \right) } }$

ただ、実際今考えているのは多重拡散項であり、最初の $FE$ は不要です。したがって、

$\displaystyle { \frac { FE }{ 1-F\left( 1-E \right) } -FE=\frac { FE }{ 1-F\left( 1-E \right) } -\frac { 1-F\left( 1-E \right) }{ 1-F\left( 1-E \right) } FE\\ =\frac { FE }{ 1-F\left( 1-E \right) } -\frac { FE-EFF\left( 1-E \right) }{ 1-F\left( 1-E \right) } =\frac { E{ F }^{ 2 }\left( 1-E \right) }{ 1-F\left( 1-E \right) } }$

ところが実際知りたかったのは、余剰分のエネルギーがフレネルの影響がどの程度あるかということであります。それは、 $\frac { E_{ fresnel } }{ E_{ no-fresnel } }$ と考えられます。なのでつまりは、

$\displaystyle { \frac { E_{ fresnel } }{ E_{ no-fresnel } } =\frac { \frac { E{ F }^{ 2 }\left( 1-E \right) }{ 1-F\left( 1-E \right) } }{ \left( 1-E \right) } =\frac { E{ F }^{ 2 } }{ 1-F\left( 1-E \right) } }$

が、欲しかった多重拡散用のフレネル項であると言えます。これをコードにすると、

inline double fresnel_avg(double n, double k) {
    return 2.0 * rt::composite_simpson<double>([&](double cosTheta) {
        return fresnel_unpolarized(n, k, cosTheta) * cosTheta;
    }, 10, 0.0, 1.0);
}

glm::dvec3 F(
    fresnel_avg(eta.r, k.r),
    fresnel_avg(eta.g, k.g),
    fresnel_avg(eta.b, k.b)
);
glm::dvec3 E = glm::dvec3(specularAlbedo);
glm::dvec3 ONE = glm::dvec3(1.0);
kLambda = E * F * F / (ONE - F * (ONE - E));

これをレンダリングすると、

f:id:ushiostarfish:20180708003629p:plain

お、わりと近いのではないでしょうか？しかしながら、ほんの僅かにα=1のとき、色が強く出すぎているような気がします。感覚的ですが、自分はいささか唐突にも感じます。どうにもF項を過剰評価しているのではないかという気がします。いっそのこと、 $F_{ avg }$ をかけるだけ、にしてみてはどうか？というアイディアがあったのでそれも試してみることにしました。

glm::dvec3 F(
    fresnel_avg(eta.r, k.r),
    fresnel_avg(eta.g, k.g),
    fresnel_avg(eta.b, k.b)
);
kLambda = F;

これらを比較してみると、 f:id:ushiostarfish:20180708003709p:plain

$F_{ avg }$ が近すぎる・・・！

別な材質、銅を試してみます。

color	n	k
R	0.23780	3.6264
G	1.0066	2.5823
B	1.2404	2.3929

※ Refractive index of Cu (Copper) - Johnson より

f:id:ushiostarfish:20180708003722p:plain

やはり $F_{ avg }$ が近すぎる・・・！自分とんでもないポカをやっているのだろうか・・・？気づいた方いらっしゃいましたらご一報いただけると嬉しいです。。

自分のレンダラーには、高ラフネス値時の色の変化がやはり唐突に感じるのと、手元のテストの結果を優先し、 $F_{ avg }$ を使うことにしました。

まとめ

[Kelemen 2001] のアプローチは大変シンプルなアイディアで、理論も軽量でありながら、相反性、エネルギー保存の問題を解消でき、さらにはエネルギー保存に一歩届かないマテリアルのエネルギー補填として、とても汎用的に使えるテクニックであるため、古い論文ながらも有用性は高いのではないでしょうか。リアルタイムレンダリングでも使えるのではないかと思います。一方でテーブルへの格納するコードは若干面倒臭く、コードも増えてしまう欠点もありますが、このあたりは解析的な関数でのフィッティングなどがあれば、いくらか良いのかもしれません。また、ここではBRDFのみにフォーカスしておりBSDFへの拡張は、おざなりでした。こちらもチャレンジの余地があります。Revisiting Physically Based Shading at Imageworks, (Christopher Kulla and Alejandro Conty) SIGGRAPH 2017 Course: Physically Based Shading in Theory and Practice - Self Shadow の[supplemental] では、Alejandro Conty Estevez, Christopher Kulla, "Production Friendly Microfacet Sheen BRDF" にて velvet-like material の中でもこの手法が使われており、こちらもチャレンジしてみるのも良さそうです。

参考画像

純粋なパストレ（10バウンス固定）, 2400x450 px, 2048spp, i7-8750Hでおのおの13分くらいです

導体

f:id:ushiostarfish:20180708002840p:plain

誘導体

f:id:ushiostarfish:20180708002720p:plain

参考文献

Csaba Kelemen and László Szirmay-Kalos, "A Microfacet Based Coupled Specular-Matte BRDF Model with Importance Sampling"

Ole Gulbrandsen Framestore, "Artist Friendly Metallic Fresnel"

Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-Scattering Microfacet BSDFs with the Smith Model"

Self Shadow, "A Multi-Faceted Exploration (Part 1)"

Self Shadow, "A Multi-Faceted Exploration (Part 2)"

PataBlog, "Multiple-Scattering BRDF"

RefractiveIndex.INFO - Refractive index database

Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs"

Revisiting Physically Based Shading at Imageworks, (Christopher Kulla and Alejandro Conty) SIGGRAPH 2017 Course: Physically Based Shading in Theory and Practice - Self Shadow

McGuire Computer Graphics Archive

2018-07-13

単位球面に対してランダムに点を生成する

Tips

概要

単位球面に対してランダムに点を生成する方法はたくさんありますが、Marsagliaの方法が大変エレガントで感動したので、それをまとめておこうと思います。

単純な方法

一つの単純な方法としては、単位球内の乱数を生成してそれを正規化することです。単位球内の乱数は、単に単位球外を棄却する方法が使えます。例えば以下のような実装が考えられます。

inline glm::dvec3 sample_on_unit_sphere(PeseudoRandom *random) {
    glm::dvec3 d;
    double sq = 0.0;
    do {
        d.x = random->uniform(-1.0, 1.0);
        d.y = random->uniform(-1.0, 1.0);
        d.z = random->uniform(-1.0, 1.0);

        sq = glm::length2(d);
    } while (sq < 1.0e-9 || 1.0 < sq);
    d /= glm::sqrt(sq);
    return d;
}

非常に直感的で、めちゃくちゃパフォーマンスが悪いかといえば、そうでもないでしょう。ただ実際成功する確率はそこそこ低く、2x2x2の立方体の体積部の単位球の体積なので、

$\displaystyle { P_{ inside }=\frac { \frac { 4 }{ 3 } \pi }{ { 2 }^{ 3 } } =\frac { 1 }{ 6 } \pi \simeq 0.523598776 }$

となり、わりと棄却されて乱数生成が無駄になっていることがわかります。実際のところ何個程度の乱数生成が必要なのか？というのの期待値を考えてみると、単位球内の乱数生成に失敗し、乱数生成が継続される確率を、

$\displaystyle { 1-\frac { 1 }{ 6 } \pi =r }$

とおくと、失敗する場合乱数が3個消費されるので、１回失敗する場合、２回失敗する場合、・・・・無限回失敗する場合全部を考えれば良いので乱数生成回数の期待値は、

$\displaystyle { N_{ avg }=3{ r }^{ 0 }+3{ r }^{ 1 }+3{ r }^{ 2 }+...3{ r }^{ \infty }\\ =3\left( { r }^{ 0 }+{ r }^{ 1 }+{ r }^{ 2 }+...{ r }^{ \infty } \right) \\ =3\sum _{ i=1 }^{ \infty }{ r } \\ =3\left( \frac { 1 }{ 1-r } \right) \\ =3\left( \frac { 1 }{ 1-\left( 1-\frac { 1 }{ 6 } \pi \right) } \right) \\ =3\left( \frac { 1 }{ \frac { 1 }{ 6 } \pi } \right) \\ =\frac { 18 }{ \pi } \simeq 5.72957795 }$

となり、実際理想的な乱数生成の個数が最低2回であることを考えると、ちょっと無駄が多い気もします。乱数生成の負荷が高い場合は、少し気になるかもしれません。（ただ乱数生成に計算負荷の高いものを使う場合、そもそも棄却するような手法を使わない気がしますが・・・）

Marsagliaの方法

Marsagliaの方法は、２つの事実を利用して、目的を達成します。

A. 単位球面に対してランダム生成された点は、それぞれ単一の軸にだけ着目すると-1~+1で密度は均一である

これはいろいろな証明方法があるようです。なれている方法で確認するとして、積分を使った方法で考えてみます。下の図のような $\theta_{end}$ で切り取られた単位球の表面積を考えてみます。

f:id:ushiostarfish:20180712232315p:plain

これは半球積分の範囲をちょっと調整すると、

$\displaystyle { \int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \theta _{ end } }{ \sin { \theta } d\theta } d\phi } \\ =2\pi \int _{ 0 }^{ \theta _{ end } }{ \sin { \theta } d\theta } \\ =2\pi \int _{ 0 }^{ \theta _{ end } }{ \sin { \theta } d\theta } }$

のように考えることができます。ここで、

$\displaystyle { x=\cos { \theta } \\ \frac { dx }{ d\theta } =-\sin { \theta } \\ -dx=\sin { \theta } d\theta }$

の変数変換を施して、

$\displaystyle { =2\pi \int _{ \cos { 0 } }^{ \cos { \theta _{ end } } }{ -x } \\ =2\pi \int _{ 1 }^{ \cos { \theta _{ end } } }{ -x } \\ =2\pi \left( \cos { \theta _{ end } } -1 \right) \left( -1 \right) \\ =2\pi \left( 1-\cos { \theta _{ end } } \right) }$

もちろん $\theta_{end} = 0$ のとき 0であり、 $\theta_{end} = \pi$ のときは $4 \pi$ であることはすぐにわかります。

ここで、 $1-\cos { \theta _{ end } }$ はなにかと考えてみると、縦の長さと捉えることができます。

f:id:ushiostarfish:20180712233531p:plain

一方 $2 \pi$ はなにかといえば、円周であり、つまり、単位球と、単位球をピッタリとすっぽりと覆う円柱の側面積とが-1~+1の任意の $\cos \theta_{ end }$ で一致することになります。

f:id:ushiostarfish:20180712234410p:plain

積分値が任意の範囲で一致するということはやはり微分値でも一致するので、言い換えれば、上の図のような配置を考える場合は、水平にどこで輪切りにしても、球面の輪切りと対応する円柱の側面積が一致するということであり、つまり面積の密度は-1~+1で均一であり、これはつまり確率も均一であるということがわかります。

※ここでは単位球で考えましたが、この性質は任意の半径で成り立ちます。

B. 単位円に対してランダム生成された点 (a, b) の $a^2+b^2$ は0~1で密度は均一である

あるrの円に、ある点(x, y) が含まれる条件は、

$\displaystyle { { x }^{ 2 }+{ y }^{ 2 }\le { r }^{ 2 } }$

となります。ここで、単位円に対してランダム生成された点 (x, y) が、ある半径r (0~1)の円に含まれている確率は、

$\displaystyle { P\left( x^{ 2 }+y^{ 2 }\le r^{ 2 } \right) =\frac { \pi r^{ 2 } }{ \pi } \\ P\left( x^{ 2 }+y^{ 2 }\le r^{ 2 } \right) =r^{ 2 } }$

と考えることができます。ここで、

$\displaystyle { x^{ 2 }+y^{ 2 }=X\\ r^{ 2 }=U }$

とでもおいてみると、

$\displaystyle { P\left( X\le U \right) =U }$

ここで、Xの範囲は0~1で、Uの範囲も0~1です。そう、つまりこれはXが 0~1に均一に分布していることを示しているわけです。

組み合わせる

単位円に均一に発生させた点を $\left( u_{ 1 },u_{ 2 } \right)$ とすると、まず簡単にわかることは、zについては、

$\displaystyle { z=1-2\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) }$

とすれば、zについては均一に-1~+1の範囲にできるので、これでOKということになります。ここで、 $u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 }$ の成分、つまり大きさ成分を使ってしまったので、正規化して向きだけのものを考えると、

$\displaystyle { \vec { u } =\frac { \left( u_{ 1 },u_{ 2 } \right) }{ \sqrt { u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } } } }$

ここで、球面上に乱数を発生させる場合の、x, y平面上のでの半径 $r_{ xy }$ は、

f:id:ushiostarfish:20180713002206p:plain

$\displaystyle { r_{ xy }=\sqrt { 1-{ z }^{ 2 } } }$

であり、これは具体的には、

$\displaystyle { r_{ xy }=\sqrt { 1-{ z }^{ 2 } } \\ =\sqrt { 1-{ \left( 1-2\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) \right) }^{ 2 } } \\ =\sqrt { 1-{ \left( 1-4\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) +4{ \left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) }^{ 2 } \right) } } \\ =\sqrt { 1-1+4\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) -4{ { \left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) }^{ 2 } } } \\ =\sqrt { 4\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) -4{ { \left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) }^{ 2 } } } \\ =2\sqrt { \left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) -{ { \left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) }^{ 2 } } } \\ =2\sqrt { \left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) \left( 1-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) \right) } \\ =2\sqrt { \left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } \sqrt { 1-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } }$

となるので、実際にほしい x, y は結局、

$\displaystyle { \vec { u_{ xy } } =\frac { \left( u_{ 1 },u_{ 2 } \right) }{ \sqrt { u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } } } r_{ xy }\\ =\frac { \left( u_{ 1 },u_{ 2 } \right) }{ \sqrt { u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } } } 2\sqrt { \left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } \sqrt { 1-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } \\ =2\left( u_{ 1 },u_{ 2 } \right) \sqrt { 1-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } }$

となるわけです。個別にかけば、

$\displaystyle { x=2u_{ 1 }\sqrt { 1-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } \\ y=2u_{ 2 }\sqrt { 1-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } \\ z=1-2\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) }$

なんてシンプルでしょうか！

プログラミング

以上をふまえ、コードを考えてみます。まずは棄却法をつかって、単位円に均一な乱数を生成します。

inline glm::dvec3 sample_on_unit_sphere(PeseudoRandom *random) {
    double x1;
    double x2;
    double S;
    do {
        x1 = random->uniform(-1.0, 1.0);
        x2 = random->uniform(-1.0, 1.0);
        S = x1 * x1 + x2 * x2;
    } while (S >= 1.0);

するとこの時点で、 $u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 }$ がすでに計算されていることに気づきます！なのでこれをそのまま使って、

inline glm::dvec3 sample_on_unit_sphere(PeseudoRandom *random) {
    double x1;
    double x2;
    double S;
    do {
        x1 = random->uniform(-1.0, 1.0);
        x2 = random->uniform(-1.0, 1.0);
        S = x1 * x1 + x2 * x2;
    } while (S >= 1.0);

    double two_sqrt_one_minus_s = 2.0 * std::sqrt(std::max(1.0 - S, 0.0));
    return glm::dvec3(
        x1 * two_sqrt_one_minus_s,
        x2 * two_sqrt_one_minus_s,
        1.0 - 2.0 * S);
}

エレガント！

f:id:ushiostarfish:20180713005833p:plain

乱数生成回数の期待値

単位円内の乱数を棄却法で生成する場合、成功する確率は、

$\displaystyle { P_{ inside }=\frac { \pi }{ { 2 }^{ 2 } } =\frac { \pi }{ { 4 } } \simeq 0.785398163 }$

であり、乱数生成が継続される確率を、

$\displaystyle { 1-\frac { \pi }{ { 4 } } =r }$

とおくと、乱数生成回数の期待値は、

$\displaystyle { N_{ avg }=2{ r }^{ 0 }+2{ r }^{ 1 }+2{ r }^{ 2 }+...2{ r }^{ \infty }\\ =2\left( { r }^{ 0 }+{ r }^{ 1 }+{ r }^{ 2 }+...{ r }^{ \infty } \right) \\ =2\sum _{ i=1 }^{ \infty }{ r } \\ =2\left( \frac { 1 }{ 1-r } \right) \\ =2\left( \frac { 1 }{ 1-\left( 1-\frac { \pi }{ { 4 } } \right) } \right) \\ =2\left( \frac { 1 }{ \frac { \pi }{ { 4 } } } \right) \\ =2\left( \frac { 4 }{ \pi } \right) \\ =\frac { 8 }{ \pi } \simeq 2.54647909 }$

であり、最初の方法に比べると乱数生成もとても少なくて済みます。

半球の場合

ついでに、上のアイディアをz+の半球の場合考えてみます。一旦zを

$\displaystyle { z=1-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) }$

として使うことにします。（わざわざ逆転させているのは、逆転させないと式が単純にならないためです）とすると、 $r_{ xy }$ は、

$\displaystyle { r_{ xy }=\sqrt { 1-{ z }^{ 2 } } \\ =\sqrt { 1-{ \left( 1-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) \right) }^{ 2 } } \\ =\sqrt { 1-\left( 1-2\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) +{ \left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) }^{ 2 } \right) } \\ =\sqrt { 2\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) -{ \left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) }^{ 2 } } \\ =\sqrt { \left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) \left( 2-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) \right) } \\ =\sqrt { u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } } \sqrt { 2-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } }$

ということはつまり、

$\displaystyle { \vec { u_{ xy } } =\frac { \left( u_{ 1 },u_{ 2 } \right) }{ \sqrt { u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } } } r_{ xy }\\ =\frac { \left( u_{ 1 },u_{ 2 } \right) }{ \sqrt { u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } } } \sqrt { u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } } \sqrt { 2-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } \\ =\left( u_{ 1 },u_{ 2 } \right) \sqrt { 2-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } }$

となり、とってもシンプルになりました！まとめると、

$\displaystyle { x=u_{ 1 }\sqrt { 2-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } \\ y=u_{ 2 }\sqrt { 2-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) } \\ z=1-\left( u_{ 1 }^{ 2 }+u_{ 2 }^{ 2 } \right) }$

これをコードにすると、

inline glm::dvec3 sample_on_unit_hemisphere(PeseudoRandom *random) {
    double x1;
    double x2;
    double S;
    do {
        x1 = random->uniform(-1.0, 1.0);
        x2 = random->uniform(-1.0, 1.0);
        S = x1 * x1 + x2 * x2;
    } while (S >= 1.0);

    double c = std::sqrt(2.0 - S);
    return glm::dvec3(
        x1 * c,
        x2 * c,
        1.0 - S);
}

となります。さらに計算が減って効率が良くなり、いい感じです！

f:id:ushiostarfish:20180714144957p:plain

参考文献

GEORGE Marsaglia, "CHOOSING A POINT FROM SURFACE OF A SPHERE"

geometry - 3 random numbers to describe point on a sphere - Mathematics Stack Exchange

2018-04-01

Microfacet入門（２）

レイトレーシング

スロープ空間

先のMicrofacet入門（１）でおざなりにしていた、 $P_{ 2 }$ とは何かについて、見ていきます。それを整理するために、まずはスロープ空間について考えます。

スロープ空間とは、マイクロファセット法線を変数変換してできる空間です。マイクロファセット法線を、 $\theta, \phi$ を使って表すと、

$\displaystyle { \omega _{ m }=\left( \cos { \phi } \sin { \theta } ,\sin { \theta } \sin { \phi } ,\cos { \theta } \right) \\ \omega _{ m }=\left( x_{ m },y_{ m },z_{ m } \right) }$

となり、スロープ空間は二次元であり、

$\displaystyle { \tilde { m } \left( \omega _{ m } \right) =\left( x_{ \tilde { m } },y_{ \tilde { m } } \right) }$

と表すことにすると、変数変換は、

$\displaystyle { \tilde { m } \left( \omega _{ m } \right) =\left( -\frac { x_{ m } }{ z_{ m } } ,-\frac { y_{ m } }{ z_{ m } } \right) \\ \tilde { m } \left( \omega _{ m } \right) =\left( -\frac { \cos { \phi } \sin { \theta } }{ \cos { \theta } } ,-\frac { \sin { \theta } \sin { \phi } }{ \cos { \theta } } \right) }$

と表すことができます。一見直観的でないように思われますが、 $\phi =-\pi$ である状況を考えてみましょう。

$\displaystyle { x_{ \tilde { m } }=-\frac { \cos { \left( -\pi \right) } \sin { \theta } }{ \cos { \theta } } =\frac { \sin { \theta } }{ \cos { \theta } } =\tan { \theta } \\ y_{ \tilde { m } }=-\frac { \sin { \theta } \sin { \left( -\pi \right) } }{ \cos { \theta } } =0 }$

なんと、x が $\tan \theta$ になりました。これが"スロープ空間"のゆえんであります。これには幾何学的解釈もでき、以下のようにスロープ空間がxy平面だとすると、z=1の面に投射した、と考えることができます。

f:id:ushiostarfish:20180401061608p:plain ※75 ページ Earl Hammon, Jr, GDC, "PBR Diffuse Lighting for GGX+Smith Microsurfaces" より

なぜかといえば、法線のxyは、zで割り算されているためで、二次元的には以下のような状態だからです。

f:id:ushiostarfish:20180401064853p:plain

ちなみに逆変換も可能で、

$\displaystyle { x_{ \tilde { m } }=-\frac { x_{ m } }{ z_{ m } } \\ y_{ \tilde { m } }=-\frac { y_{ m } }{ z_{ m } } \\ -x_{ \tilde { m } }z_{ m }=x_{ m }\\ -y_{ \tilde { m } }z_{ m }=y_{ m } }$

であるため、法線 $\omega _m$ は、

$\displaystyle { \omega _{ m }=\left( -x_{ \tilde { m } }z_{ m },-y_{ \tilde { m } }z_{ m },z_{ m } \right) }$

ただ、 $z_{ m }$ は未知であり、

$\displaystyle { \left| \omega _{ m } \right| =\sqrt { { x_{ m } }^{ 2 }+{ y_{ m } }^{ 2 }+{ z_{ m } }^{ 2 } } =1\\ \sqrt { { \left( x_{ \tilde { m } }z_{ m } \right) }^{ 2 }+{ \left( y_{ \tilde { m } }z_{ m } \right) }^{ 2 }+{ z_{ m } }^{ 2 } } =1\\ { \left( x_{ \tilde { m } }z_{ m } \right) }^{ 2 }+{ \left( y_{ \tilde { m } }z_{ m } \right) }^{ 2 }+{ z_{ m } }^{ 2 }=1\\ { \left( x_{ \tilde { m } } \right) }^{ 2 }+{ \left( y_{ \tilde { m } } \right) }^{ 2 }+1=\frac { 1 }{ { z_{ m } }^{ 2 } } \\ { z_{ m } }^{ 2 }=\frac { 1 }{ { \left( x_{ \tilde { m } } \right) }^{ 2 }+{ \left( y_{ \tilde { m } } \right) }^{ 2 }+1 } \\ { z_{ m } }=\frac { 1 }{ \sqrt { { \left( x_{ \tilde { m } } \right) }^{ 2 }+{ \left( y_{ \tilde { m } } \right) }^{ 2 }+1 } } }$

とすると、求めることができるため、最終的には、

$\displaystyle { \omega _{ m }=\frac { 1 }{ \sqrt { { \left( x_{ \tilde { m } } \right) }^{ 2 }+{ \left( y_{ \tilde { m } } \right) }^{ 2 }+1 } } \left( -x_{ \tilde { m } },-y_{ \tilde { m } },1 \right) }$

となります。法線が逆側の場合はどうか？というのもありますが、実際ミクロ表面は裏返らないため、問題ありません。

スロープ空間とヤコビアン

変換方法は明らかになりましたが、元の"法線分布"を引き継ぐため、この変数変換のヤコビアンを求めておきたいです。もとの変数は $\theta, \phi$ であり、ここから $x_{ \tilde { m } },y_{ \tilde { m } }$ への変換は、ヤコビ行列は、

$\displaystyle { J=\begin{pmatrix} \frac { \partial x_{ \tilde { m } } }{ \partial \theta } & \frac { \partial x_{ \tilde { m } } }{ \partial \phi } \\ \frac { \partial y_{ \tilde { m } } }{ \partial \theta } & \frac { \partial y_{ \tilde { m } } }{ \partial \phi } \end{pmatrix}=\begin{pmatrix} -\cos \left( \phi \right) \sec ^{ 2 } \left( \theta \right) & \sin \left( \phi \right) \tan \left( \theta \right) \\ -\sin \left( \phi \right) \sec ^{ 2 } \left( \theta \right) & -\tan \left( \theta \right) \cos \left( \phi \right) \end{pmatrix} }$

と、これは機械的に求め、ここからヤコビアンは、

$\displaystyle { \left| J \right| =\cos \left( \phi \right) \sec ^{ 2 } \left( \theta \right) \tan \left( \theta \right) \cos \left( \phi \right) +\sin \left( \phi \right) \tan \left( \theta \right) \sin \left( \phi \right) \sec ^{ 2 } \left( \theta \right) \\ =\cos ^{ 2 } \left( \phi \right) \sec ^{ 2 } \left( \theta \right) \tan \left( \theta \right) +\sin ^{ 2 } \left( \phi \right) \sec ^{ 2 } \left( \theta \right) \tan \left( \theta \right) \\ =\sec ^{ 2 } \left( \theta \right) \tan \left( \theta \right) \left( \cos ^{ 2 } \left( \phi \right) +\sin ^{ 2 } \left( \phi \right) \right) \\ =\frac { 1 }{ \cos ^{ 2 }{ \theta } } \frac { \sin { \theta } }{ \cos { \theta } } \\ =\frac { \sin { \theta } }{ \cos ^{ 3 }{ \theta } } }$

と求めることができます。ヤコビアンは微小な成分の拡大率であるため、以下のように積分の辻褄があったまま変数変換することができます。

$\displaystyle { \int _{ -\infty }^{ +\infty }{ \int _{ -\infty }^{ +\infty }{ f\left( x_{ \tilde { m } },y_{ \tilde { m } } \right) dx_{ \tilde { m } } } dy_{ \tilde { m } } } =\int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ f\left( \theta ,\phi \right) \frac { \sin { \theta } }{ \cos ^{ 3 }{ \theta } } d\theta d\phi } } }$

これを使って、

$\displaystyle { 1=\int _{ \Omega }^{ }{ D\left( \omega _{ m } \right) \left| \omega _{ m }\cdot \omega _{ g } \right| d\omega _{ m } } \\ 1=\int _{ -\infty }^{ +\infty }{ \int _{ -\infty }^{ +\infty }{ { P }^{ 22 }\left( x_{ \tilde { m } },y_{ \tilde { m } } \right) dx_{ \tilde { m } } } dy_{ \tilde { m } } } }$

を満たすような ${ P }^{ 22 }$ を考えます。これには、

$\displaystyle { \int _{ \Omega }^{ }{ D\left( \omega _{ m } \right) \left| \omega _{ m }\cdot \omega _{ g } \right| d\omega _{ m } } ={ \int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ D\left( \omega _{ m } \right) \cos { \theta } \sin { \theta } d\theta d\phi } } } }$

であり、

$\displaystyle { \int _{ -\infty }^{ +\infty }{ \int _{ -\infty }^{ +\infty }{ { P }^{ 22 }\left( x_{ \tilde { m } },y_{ \tilde { m } } \right) dx_{ \tilde { m } } } dy_{ \tilde { m } } } =\int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ { P }^{ 22 }\left( x_{ \tilde { m } },y_{ \tilde { m } } \right) \frac { \sin { \theta } }{ \cos ^{ 3 }{ \theta } } d\theta d\phi } } }$

であることから、

$\displaystyle { { P }^{ 22 }\left( x_{ \tilde { m } },y_{ \tilde { m } } \right) \frac { \sin { \theta } }{ \cos ^{ 3 }{ \theta } } =D\left( \omega _{ m } \right) \cos { \theta } \sin { \theta } \\ { P }^{ 22 }\left( x_{ \tilde { m } },y_{ \tilde { m } } \right) =D\left( \omega _{ m } \right) \cos ^{ 4 }{ \theta } }$

のようにDから機械的に変換することができることがわかります。

具体的なP

そろそろ具体的なDを考えて、そこからPを出しておきましょう。有名な法線分布として今回は、Beckmann分布と、GGX(Trowbridge-Reitz)分布を取り上げます。まずBeckmann分布ですが、これの具体的な形は $\alpha$ をパラメーターとして、

$\displaystyle { D_{ beckmann }\left( \omega _{ m } \right) =\frac { { \chi }^{ + }\left( \omega _{ m }\cdot \omega _{ g } \right) }{ \pi { \alpha }^{ 2 }\cos ^{ 4 }{ \theta } } exp\left( -\frac { \tan ^{ 2 }{ \theta } }{ { \alpha }^{ 2 } } \right) }$

ここから ${ P }^{ 22 }$ は、

$\displaystyle { { P }^{ 22 }\left( x_{ \tilde { m } },y_{ \tilde { m } } \right) =\frac { 1 }{ \pi { \alpha }^{ 2 } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 }+{ y_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) }$

となります。 ${ x_{ \tilde { m } } }^{ 2 }+{ y_{ \tilde { m } } }^{ 2 }$ はスロープ空間上でのゼロ地点からの距離の二乗であり、それは結局 $\tan^2 \theta$ であることを利用しています。

そう、なんとBeckmann分布はスロープ空間において、標準的な2次元ガウス関数だったのです。

続いて、GGX(Trowbridge-Reitz)分布です。

$\displaystyle { D_{ ggx }\left( \omega _{ m } \right) =\frac { { \chi }^{ + }\left( \omega _{ m }\cdot \omega _{ g } \right) }{ \pi { \alpha }^{ 2 }\cos ^{ 4 }{ \theta _{ m } } { \left( 1+\frac { \tan ^{ 2 }{ \theta _{ m } } }{ { \alpha }^{ 2 } } \right) }^{ 2 } } }$

こちらも同様に、

$\displaystyle { { P }^{ 22 }\left( x_{ \tilde { m } },y_{ \tilde { m } } \right) =\frac { 1 }{ \pi { \alpha }^{ 2 }{ \left( 1+\frac { { x_{ \tilde { m } } }^{ 2 }+{ y_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) }^{ 2 } } }$

となります。

P2

では Microfacet入門（１）での $P_{ 2 }$ は結局何かと言えば、片方を単純に積分して一次元に落としたものです。

$\displaystyle { { P }^{ 2- }\left( x_{ \tilde { m } } \right) =\int _{ -\infty }^{ \infty }{ { P }^{ 22 }\left( x_{ \tilde { m } },y_{ \tilde { m } } \right) dy_{ \tilde { m } } } }$

これは実際のところ、Beckmann分布とGGX(Trowbridge-Reitz)分布で解析的に解くことができ、

Beckmann分布の場合は、

$\displaystyle { \\ { P }^{ 2- }\left( x_{ \tilde { m } } \right) =\frac { 1 }{ \pi { \alpha }^{ 2 } } \int _{ -\infty }^{ \infty }{ exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } -\frac { { y_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dy_{ \tilde { m } } } \\ =\frac { 1 }{ \pi { \alpha }^{ 2 } } \int _{ -\infty }^{ \infty }{ exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } -\frac { { y_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dy_{ \tilde { m } } } \\ =\frac { 1 }{ \pi { \alpha }^{ 2 } } \int _{ -\infty }^{ \infty }{ exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } -\frac { { y_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dy_{ \tilde { m } } } \\ =\frac { 1 }{ \pi { \alpha }^{ 2 } } \int _{ -\infty }^{ \infty }{ exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) exp\left( -\frac { { y_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dy_{ \tilde { m } } } \\ =\frac { 1 }{ \pi { \alpha }^{ 2 } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) \int _{ -\infty }^{ \infty }{ exp\left( -\frac { { y_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dy_{ \tilde { m } } } \\ =\frac { 1 }{ \pi { \alpha }^{ 2 } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) \sqrt { \pi { \alpha }^{ 2 } } \\ =\frac { \sqrt { \pi { \alpha }^{ 2 } } }{ \pi { \alpha }^{ 2 } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) \\ =\frac { \sqrt { \pi { \alpha }^{ 2 } } \sqrt { \pi { \alpha }^{ 2 } } }{ \sqrt { \pi { \alpha }^{ 2 } } \pi { \alpha }^{ 2 } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) \\ =\frac { \pi { \alpha }^{ 2 } }{ \sqrt { \pi { \alpha }^{ 2 } } \pi { \alpha }^{ 2 } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) \\ =\frac { 1 }{ \sqrt { \pi { \alpha }^{ 2 } } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) \\ }$

となります。

GGX分布の場合は...すみません、自分の積分力の欠如により、Symbolab Math Solver - Step by Step calculator で自動で解くと、

www.symbolab.com

$\displaystyle { { P }^{ 2- }\left( x_{ \tilde { m } } \right) =\int _{ -\infty }^{ \infty }{ \frac { 1 }{ \pi { \alpha }^{ 2 }\left( 1+\frac { { x_{ \tilde { m } } }^{ 2 }+{ y_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) } dy_{ \tilde { m } } } \\ { P }^{ 2- }\left( x_{ \tilde { m } } \right) =\frac { \alpha ^{ 2 } }{ 2\left( x_{ \tilde { m } }^{ 2 }+\alpha ^{ 2 } \right) ^{ \frac { 3 }{ 2 } } } }$

のようになります。

Λ （Beckmann分布）

先のMicrofacet入門（１）では、もう一つおざなりにしていたのは $\Lambda$ です。

$\displaystyle { \Lambda \left( \mu \right) =\frac { 1 }{ \mu } \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } \\ \Lambda \left( \omega _{ o } \right) =\frac { 1 }{ \cot { \theta _{ o } } } \int _{ \cot { \theta _{ o } } }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\cot { \theta _{ o } } \right) dq } }$

こちらも、なんと、解析的に解くことができます。 Beckmann分布の場合、

$\displaystyle { { P }^{ 2- }\left( x_{ \tilde { m } } \right) =\frac { 1 }{ \sqrt { \pi { \alpha }^{ 2 } } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) \\ \Lambda =\frac { 1 }{ \cot { \theta _{ o } } } \int _{ \cot { \theta _{ o } } }^{ +\infty }{ \left( x_{ \tilde { m } }-\cot { \theta _{ o } } \right) { P }^{ 2- }\left( x_{ \tilde { m } } \right) dx_{ \tilde { m } } } \\ =\frac { 1 }{ \cot { \theta _{ o } } } \int _{ \cot { \theta _{ o } } }^{ +\infty }{ \left( x_{ \tilde { m } }-\cot { \theta _{ o } } \right) \frac { 1 }{ \sqrt { \pi { \alpha }^{ 2 } } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dx_{ \tilde { m } } } \\ =\frac { 1 }{ \cot { \theta _{ o } } } \int _{ \cot { \theta _{ o } } }^{ +\infty }{ x_{ \tilde { m } }\frac { 1 }{ \sqrt { \pi { \alpha }^{ 2 } } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) -\cot { \theta _{ o } } \frac { 1 }{ \sqrt { \pi { \alpha }^{ 2 } } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dx_{ \tilde { m } } } \\ =\frac { 1 }{ \cot { \theta _{ o } } } \int _{ \cot { \theta _{ o } } }^{ +\infty }{ x_{ \tilde { m } }\frac { 1 }{ \sqrt { \pi { \alpha }^{ 2 } } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dx_{ \tilde { m } } } -\frac { 1 }{ \cot { \theta _{ o } } } \int _{ \cot { \theta _{ o } } }^{ +\infty }{ \cot { \theta _{ o } } \frac { 1 }{ \sqrt { \pi { \alpha }^{ 2 } } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dx_{ \tilde { m } } } \\ =\frac { 1 }{ \cot { \theta _{ o } } } \int _{ \cot { \theta _{ o } } }^{ +\infty }{ x_{ \tilde { m } }\frac { 1 }{ \sqrt { \pi { \alpha }^{ 2 } } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dx_{ \tilde { m } } } -\int _{ \cot { \theta _{ o } } }^{ +\infty }{ \frac { 1 }{ \sqrt { \pi { \alpha }^{ 2 } } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dx_{ \tilde { m } } } \\ }$

この後、左と右の項をそれぞれまた Symbolab Math Solver - Step by Step calculatorの力を借りて、

$\displaystyle { a=\frac { 1 }{ \alpha \tan { \theta } } =\frac { \cot \theta }{ \alpha } }$

と置きながら...

左の項 www.symbolab.com

$\displaystyle { \frac { 1 }{ \cot { \theta _{ o } } } \int _{ \cot { \theta _{ o } } }^{ +\infty }{ x_{ \tilde { m } }\frac { 1 }{ \sqrt { \pi { \alpha }^{ 2 } } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dx_{ \tilde { m } } } =\frac { \sqrt { \alpha ^{ 2 } } \tan \left( θ \right) e^{ -\frac { \cot ^{ 2 } \left( θ \right) }{ a^{ 2 } } } }{ 2\sqrt { \pi } } \\ \\ a=\frac { 1 }{ \alpha \tan { \theta } } =\frac { \cot \theta }{ \alpha } \\ \alpha =\frac { 1 }{ a\tan { \theta } } \\ \\ =\frac { \frac { 1 }{ a\tan { \theta } } \tan \left( θ \right) e^{ -{ a }^{ 2 } } }{ 2\sqrt { \pi } } \\ =\frac { 1 }{ 2a\sqrt { \pi } } e^{ -{ a }^{ 2 } } }$

右の項

www.symbolab.com

$\displaystyle { \int _{ \cot { \theta _{ o } } }^{ +\infty }{ \frac { 1 }{ \sqrt { \pi { \alpha }^{ 2 } } } exp\left( -\frac { { x_{ \tilde { m } } }^{ 2 } }{ { \alpha }^{ 2 } } \right) dx_{ \tilde { m } } } =\frac { 1 }{ 2 } -\frac { \alpha { erf }\left( \frac { \cot \left( θ \right) }{ \alpha } \right) }{ 2\sqrt { \alpha ^{ 2 } } } \\ \\ \\ a=\frac { 1 }{ \alpha \tan { \theta } } =\frac { \cot \theta }{ \alpha } \\ \\ =\frac { 1 }{ 2 } -\frac { \alpha { erf }\left( a \right) }{ 2\alpha } \\ =\frac { 1 }{ 2 } -\frac { { erf }\left( a \right) }{ 2 } \\ =\frac { 1-erf\left( a \right) }{ 2 } \\ }$

したがって、まとめると、

$\displaystyle { \Lambda \left( \omega _{ o } \right) =\frac { 1 }{ 2a\sqrt { \pi } } e^{ -{ a }^{ 2 } }-\frac { 1-erf\left( a \right) }{ 2 } \\ \Lambda \left( \omega _{ o } \right) =\frac { 1 }{ 2a\sqrt { \pi } } e^{ -{ a }^{ 2 } }+\frac { erf\left( a \right) -1 }{ 2 } }$

ただし、

$\displaystyle { a=\frac { 1 }{ \alpha \tan { \theta } } =\frac { \cot \theta }{ \alpha } }$

と求めることができました。

Λ （GGX分布）

GGX分布の場合のΛは、

ここでまたまたSymbolab Math Solver - Step by Step calculatorの力を借りて、

www.symbolab.com

$\displaystyle { { P }^{ 2- }\left( x_{ \tilde { m } } \right) =\frac { \alpha ^{ 2 } }{ 2\left( x_{ \tilde { m } }^{ 2 }+\alpha ^{ 2 } \right) ^{ \frac { 3 }{ 2 } } } \\ \Lambda =\frac { 1 }{ \cot { \theta _{ o } } } \int _{ \cot { \theta _{ o } } }^{ +\infty }{ \left( x_{ \tilde { m } }-\cot { \theta _{ o } } \right) \frac { \alpha ^{ 2 } }{ 2\left( x_{ \tilde { m } }^{ 2 }+\alpha ^{ 2 } \right) ^{ \frac { 3 }{ 2 } } } dx_{ \tilde { m } } } \\ \\ { P }^{ 2- }\left( x_{ \tilde { m } } \right) =\frac { \alpha ^{ 2 } }{ 2\left( x_{ \tilde { m } }^{ 2 }+\alpha ^{ 2 } \right) ^{ \frac { 3 }{ 2 } } } \\ \Lambda =\frac { 1 }{ \cot { \theta _{ o } } } \int _{ \cot { \theta _{ o } } }^{ +\infty }{ \left( x_{ \tilde { m } }-\cot { \theta _{ o } } \right) { P }^{ 2- }\left( x_{ \tilde { m } } \right) dx_{ \tilde { m } } } \\ =\frac { 1 }{ 2 } \tan \left( θ \right) \left( \sqrt { a^{ 2 }+\cot ^{ 2 } \left( θ \right) } -\cot \left( θ \right) \right) \\ =\frac { 1 }{ 2 } \tan \left( θ \right) \left( \sqrt { \left( \frac { 1 }{ \alpha \tan { \theta } } \right) ^{ 2 }+\left( \frac { 1 }{ \tan { \theta } } \right) ^{ 2 } } -\frac { 1 }{ \tan { \theta } } \right) \\ =\frac { 1 }{ 2 } \tan \left( θ \right) \left( \sqrt { \left( \frac { 1 }{ \tan { \theta } } \right) ^{ 2 }\left( \frac { 1 }{ \alpha } +1 \right) } -\frac { 1 }{ \tan { \theta } } \right) \\ =\frac { 1 }{ 2 } \tan \left( θ \right) \left( \frac { 1 }{ \tan { \theta } } \sqrt { \frac { 1 }{ \alpha } +1 } -\frac { 1 }{ \tan { \theta } } \right) \\ =\frac { 1 }{ 2 } \tan \left( θ \right) \left( \frac { 1 }{ \tan { \theta } } \left( \sqrt { \frac { 1 }{ \alpha } +1 } -1 \right) \right) \\ =\frac { 1 }{ 2 } \left( \sqrt { \frac { 1 }{ \alpha } +1 } -1 \right) \\ =\frac { -1+\sqrt { \frac { 1 }{ \alpha } +1 } }{ 2 } \\ }$

ただし、

$\displaystyle { a=\frac { 1 }{ \alpha \tan { \theta } } =\frac { \cot \theta }{ \alpha } }$

と求めることができました。

実装例

 inline double chi_plus(double x) {
        return x < 0.0 ? 0.0 : 1.0;
    }
    inline double D_Beckman(const Vec3 &n, const Vec3 &h, double alpha) {
        double cosTheta = glm::dot(n, h);
        if (cosTheta < 1.0e-9) {
            return 0.0;
        }
        double cosTheta2 = cosTheta * cosTheta;
        double cosTheta4 = cosTheta2 * cosTheta2;
        double alpha2 = alpha * alpha;
        double chi = chi_plus(cosTheta);

        // \tan { \theta  } =\pm \frac { \sqrt { 1-\cos { \theta  }  }  }{ \cos { \theta  }  } \\ \tan ^{ 2 }{ \theta  } =\frac { 1-\cos ^{ 2 }{ \theta  }  }{ \cos ^{ 2 }{ \theta  }  } 
        double tanTheta2 = (1.0 - cosTheta2) / cosTheta2;
        return chi * std::exp(-tanTheta2 / alpha2) / (glm::pi<double>() * alpha2 * cosTheta4);
    }
    inline double D_GGX(const Vec3 &n, const Vec3 &h, double alpha) {
        double cosTheta = glm::dot(n, h);
        if (cosTheta < 1.0e-9) {
            return 0.0;
        }
        double cosTheta2 = cosTheta * cosTheta;
        double cosTheta4 = cosTheta2 * cosTheta2;
        double alpha2 = alpha * alpha;
        double chi = chi_plus(cosTheta);

        // \tan { \theta  } =\pm \frac { \sqrt { 1-\cos { \theta  }  }  }{ \cos { \theta  }  } \\ \tan ^{ 2 }{ \theta  } =\frac { 1-\cos ^{ 2 }{ \theta  }  }{ \cos ^{ 2 }{ \theta  }  } 
        double tanTheta2 = (1.0 - cosTheta2) / cosTheta2;
        return chi / (glm::pi<double>() * alpha2 * cosTheta4 * Sqr(1.0 + tanTheta2 / alpha2));
    }

    inline double lambda_beckmann(double cosTheta, double alpha) {
        double tanThetaO = std::sqrt(1.0 - cosTheta * cosTheta) / cosTheta;
        double a = 1.0 / (alpha * tanThetaO);
        return (std::erf(a) - 1.0) * 0.5 + std::exp(-a * a) / (2.0 * a * std::sqrt(glm::pi<double>()));
    }
    inline double lambda_ggx(double cosTheta, double alpha) {
        double tanThetaO = std::sqrt(1.0 - cosTheta * cosTheta) / cosTheta;
        double a = 1.0 / (alpha * tanThetaO);
        return -1.0 + std::sqrt(1.0 + 1.0 / (a * a)) * 0.5;
    }

    inline double G_2_beckmann(const Vec3 &omega_i, const Vec3 &omega_o, const Vec3 &omega_h, const Vec3 &n, double alpha) {
        double numer = chi_plus(glm::dot(omega_o, omega_h)) * chi_plus(glm::dot(omega_i, omega_h));
        double denom = (1.0 + lambda_beckmann(glm::dot(omega_o, n), alpha) + lambda_beckmann(glm::dot(omega_i, n), alpha));
        return numer / denom;
    }

    inline double G_2_ggx(const Vec3 &omega_i, const Vec3 &omega_o, const Vec3 &omega_h, const Vec3 &n, double alpha) {
        double numer = chi_plus(glm::dot(omega_o, omega_h)) * chi_plus(glm::dot(omega_i, omega_h));
        double denom = (1.0 + lambda_ggx(glm::dot(omega_o, n), alpha) + lambda_ggx(glm::dot(omega_i, n), alpha));
        return numer / denom;
    }

f:id:ushiostarfish:20180401085858p:plain

まとめ

マイクロファセットBRDFの理論的背景は、驚くほどに緻密で、なかなかとっつきづらいものでした。しかしひとつひとつ紐解けば、その洞察の一つ一つが結構刺激的で面白いことに気づきます。発展手法を追いかけるためにも、一度その深みに触れてみるのもよいかもしれません。

参考文献

Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs"

Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces"

Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-scattering microfacet BSDFs with the Smith model"

Earl Hammon, Jr, GDC, "PBR Diffuse Lighting for GGX+Smith Microsurfaces"

Microfacetモデルの重点サンプリング

脱・完全鏡面反射～GGXについて調べてみた～

鏡面BRDF

2018-03-18

Microfacet入門（１）

レイトレーシング

動機

現在リアルタイムレンダリング、およびオフラインレンダリングにて、マイクロファセット理論をベースにした材質の表現は幅広く使われています。また、それらをベースにした発展手法も数多く存在し、それらを追いかけていく上でも基礎理論を整理しておくことは重要のように思われます。しかしながら、マイクロファセットベースのBRDF&BSDFによく使われる式そのものの情報は数多くあるにも関わらず、それらの導出の部分に関する資料はかなり少ないように思いました。そこで本稿ではマイクロファセット理論に関する論文である、

Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs"

Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces"

をベースに紐解いていくことを目標にしようと思います。ただ、基本的には前者を追いかけるような形になります。ただ省略している部分もありますので、原著をあたっていただくと、どこが省略されているのかが丸見えになるので、合わせて参照していただくのが良いと思います。

Microfacet

マイクロファセット理論では、まず反射の複雑なふるまいは物体表面の微小な法線の分布によって起こると仮定しています。そこで何かしら基準となる空間を設けたいところです。慣習的には、面積が1である幾何学平面(geometric surface) を基準に、そこに凸凹したマイクロサーフェス(microsurface)を配置したモデルを使います。

f:id:ushiostarfish:20180321173208p:plain

※ Figure 2. The geometric surface and the microsurface. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

$M$ はマイクロサーフェスの領域、 $\omega_g$ は幾何学平面の法線、 $p_m$ がマイクロサーフェス上の点、 $\omega_m$ その点の法線を表しています。

即座にわかるポイントとしては、多少なりともでこぼこしたマイクロサーフェスの面積は全部集めてくると１を超えてしまうということがわかります。

投影面積

ここでちょっと図のようなマイクロサーフェスから、ある方向 $\omega_o$ への出射放射輝度を考えてみます。

f:id:ushiostarfish:20180321201952p:plain ※ Figure 1. The outgoing radiance of surfaceMis the average of the radiances from each point of the surface, weighted by their projected-area fractions towards the outgoing direction. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

まずはM全域にわたって放射輝度を集める必要があるため、積分を以下のように考えます。

$\displaystyle { \int _{ M }^{ }{ projected\ area\left( p_{ m } \right) L\left( \omega _{ o },p_{ m } \right) dp_{ m } } }$

ここで放射輝度は"見えている面積の分"だけ集めるため、投射された面積を基準にする必要があります。ここで投射であるため、 $cos \theta$ 使いたくなりますが、わざわざprojected areaとしているのは、隣接するマイクロサーフェスに遮蔽されるようなケースもあるため、ここでは文字で記述されています。

しかしまだこれではマイクロサーフェス上の面積範囲で積分してしまっているので出射放射輝度にはなりませんので、出射放射輝度とするために、投影面積で割ることで平均放射輝度としてあげる必要があります。それを付け加えると、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { \int _{ M }^{ }{ projected\ area\left( p_{ m } \right) L\left( \omega _{ o },p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ projected\ area\left( p_{ m } \right) dp_{ m } } } }$

となります。この考察から、

隣接するマイクロサーフェスに遮蔽される
投影

といったところが後々キーポイントになるであろうともわかってきます。

マイクロサーフェスと立体角

ベースとなるマイクロサーフェスが定義できましたが、実際のところ今後更なる解析を進めていくにあたって、マイクロサーフェスを立体角ベースでも考えていけると便利です。そこで何らかの形でマイクロサーフェスと立体角を結び付けておく必要があります。そこで、立体角を与えたらマイクロサーフェスの面積が返ってくる（この場合単位は $m^2/sr$ になりますね）-そんな関数を定義します。

$\displaystyle { D\left( \omega \right) =\int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } }$

ここで $\omega _{ m }\left( p_{ m } \right)$ はある点の法線であり、 $\delta \left( \right)$ は次元が $1/sr$ のデルタ関数であり、法線が一致しているところにピークが存在しています。

なんだかニュアンスは分からなくはないような・・・？分からないような気がします。そこで、ここではある任意の立体角の範囲での積分を考えてみます。

$\displaystyle { \int _{ \Omega _{ Any } }^{ }{ D\left( \omega \right) d\omega } \\ =\int _{ \Omega _{ Any } }^{ }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } d\omega } \\ =\int _{ M }^{ }{ \int _{ \Omega _{ Any } }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) d\omega } dp_{ m } } }$

ここで、

$\displaystyle { \int _{ \Omega _{ Any } }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) d\omega } }$

の部分に着目すると、デルタ関数は単体での積分結果は、範囲に含まれていれば1、そうでなければ0になります。つまり、Dを立体角で積分すると、その立体角に収まるような法線を持つマイクロサーフェスの面積になる、ということになります。このようにつじつまが合うように考えられた定義である、ということです。

もちろん全立体角の積分は、マイクロサーフェス全体の面積に一致します。

$\displaystyle { microsurface\ area=\int _{ M }^{ }{ dp_{ m } } =\int _{ \Omega }^{ }{ D\left( \omega _{ m } \right) d\omega _{ m } } }$

マイクロサーフェス上の積分から、立体角上の積分へ

先の節の拡張として、マイクロサーフェス上の関数を考えた場合、それを立体角に持っていくとき、

$\displaystyle { \int _{ M }^{ }{ g\left( p_{ m } \right) dp_{ m } } =\int _{ \Omega }^{ }{ g\left( \omega _{ m } \right) D\left( \omega _{ m } \right) d\omega _{ m } } }$

を満たすような $g\left( p_{ m } \right)$ と $g\left( \omega _{ m } \right)$ の関係性はどういったものでしょうか？やや天下り的ですが、以下のように結びつけるとうまくいきます。

$\displaystyle { g\left( \omega \right) =\frac { \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) g\left( p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } } }$

これは D と gをそれぞれ代入していくと確認することができます。

$\displaystyle { \int _{ \Omega }^{ }{ g\left( \omega _{ m } \right) D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \frac { \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) g\left( p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } } \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) g\left( p_{ m } \right) dp_{ m } } d\omega _{ m } } \\ =\int _{ M }^{ }{ \int _{ \Omega }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) g\left( p_{ m } \right) dp_{ m } } d\omega _{ m } } \\ =\int _{ M }^{ }{ g\left( p_{ m } \right) d\omega _{ m } } }$

なるほど、確かにうまく定義したものです。

幾何学平面への投影

ここでもう一度先のマイクロサーフェスの図を確認してみます

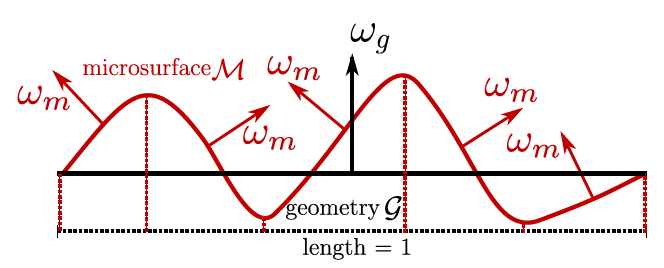f:id:ushiostarfish:20180321210211p:plain ※ Figure 3. (a) Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

マイクロサーフェス全体の面積は不明ですが、しかし幾何学平面gの面積は1にしていました。つまり、内積を使って幾何学平面に投射を考えてみると、以下の式が成り立つことがわかります。

$\displaystyle { \int _{ M }^{ }{ \omega _{ g }\cdot \omega _{ m }\left( p_{ m } \right) dp_{ m } } =1 }$

さらに、半球での積分を考えても、

$\displaystyle { \int _{ \Omega }^{ }{ \omega _{ g }\cdot \omega _{ m }D\left( \omega _{ m } \right) d\omega _{ m } } =1 }$

また同様のことを表している、ということになります。実際、具体的なD、たとえばBeckmann分布や、GGX分布を試しに数値積分してみると、確かに1になることを確認することもできます。

出射方向の投射面積

幾何学平面への投射ついでに、任意の出射方向への投射を一緒に考えておきましょう。まずは幾何学平面そのものの投射です。

f:id:ushiostarfish:20180324174447p:plain ※ Figure 3. (b) Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

幾何学平面の面積は1でした。したがって、その投射は当然 $\cos \theta$ および内積で表すことができます。

$\displaystyle { \int _{ \Omega }^{ }{ \omega _{ g }\cdot \omega _{ m }D\left( \omega _{ m } \right) d\omega _{ m } } =1 }$

ここでさらにマイクロサーフェスの投射を考えてみます。

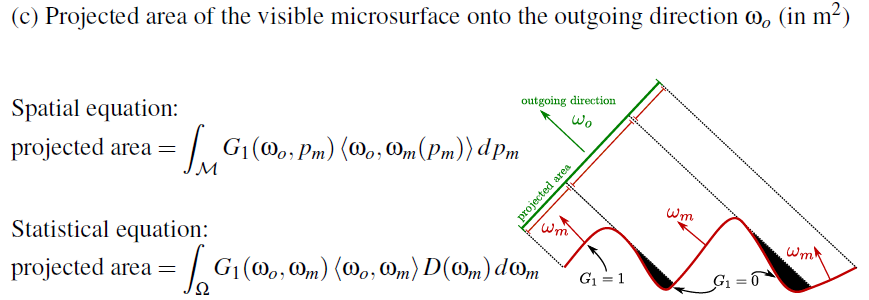f:id:ushiostarfish:20180324180225p:plain ※ Figure 3. (c) Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

$\lt \omega _{ o },\omega _{ m } \gt$ の部分は内積を正にクランプしたものを表しており、面積の投射を表現しています。つぎにGですが、空間ベース(Spatial) の方程式の $G_1\left( \omega_{ o },p_{ m } \right)$ はマイクロサーフェス上のある点が見えていれば1を、隠れていれば0 を返す関数です。一方、統計ベース(Statistical)の方程式の $G_1\left( \omega _{ o },\omega _{ m } \right)$ は、ある方向の法線を持つマイクロサーフェスのうち、何割が隠れているか？を表す関数です。尺度は違っていても、まったく同様の現象を表していることになります。

出射方向の投射面積の投射面積の表現の仕方が２種類あることがわかりました。そこで、投影面積の関係式が導かれます。

これがいわゆる単一方向のMasking Functionであり、具体的なGの内容を考える際には、この方程式を満たすかどうか？重要なポイントになってきます。ついでに、何割が隠れているか？というとちょっとふわっとしていたため、 $G_1\left( \omega _{ o },\omega _{ m } \right)$ を式として表現すると、マイクロサーフェス上の積分から、立体角上の積分への操作により、以下のように表現できます。

$\displaystyle { G_1\left( \omega _{ o },\omega _{ m } \right) =\frac { \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } } }$

※なんとなく、"遮蔽の割合"の意味が式から感じられる気がします

一応実際にこのバージョンでも確認してみると、

$\displaystyle { \cos { \theta _{ o } } =\int _{ \Omega }^{ }{ G_1\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \frac { \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } } \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \frac { \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } } \left< \omega _{ o },\omega _{ m } \right> \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) dp_{ m } } \left< \omega _{ o },\omega _{ m } \right> d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) \left< \omega _{ o },\omega _{ m } \right> dp_{ m } } d\omega _{ m } } \\ =\int _{ M }^{ }{ \int _{ \Omega }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) \left< \omega _{ o },\omega _{ m } \right> d\omega _{ m } } dp_{ m } } \\ =\int _{ M }^{ }{ G_1\left( \omega _{ o },p_{ m } \right) \left< \omega _{ o },\omega _{ m } \right> dp_{ m } } }$

確かになりました。

マスキング関数は一意に定まるか？

先の投影面積の関係式、

と、任意のDがあれば、Gは一意に定まるんでしょうか？定まるとしたら、便利です。しかし実際は定まりません。以下の図を見てみましょう。

f:id:ushiostarfish:20180324200455p:plain ※ Figure 4. Microsurfaces with the same distribution of normals but with different profiles result in different BRDFs. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

図では法線分布が同じ２つの表面を比較しています。例えば赤が完全に隠れていたり、完全に見えたりしています。つまり表面の構造(論文中ではthe microsurface profileと呼ばれています)によって性質が異なってきてしまうのです。これは何を意味するかというと、Gを考えるときには、

"なんらかの仮定して、Gを導出する"

というプロセスが必要ということになります。このプロセスの違いが SmithのモデルだったりV-cavityだったりなどするということです。

放射輝度

最初に提示していたマイクロサーフェスからの放射輝度をもう一度見てみると、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { \int _{ M }^{ }{ projectedarea\left( p_{ m } \right) L\left( \omega _{ o },p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ projectedarea\left( p_{ m } \right) dp_{ m } } } }$

すでにいくつかの考察により、既知の量があり、それに乗り換えてみます。まずは分母の投影面積は、 $\cos \theta$ だったので、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { 1 }{ \cos { \theta _{ o } } } \int _{ M }^{ }{ projectedarea\left( p_{ m } \right) L\left( \omega _{ o },p_{ m } \right) dp_{ m } } }$

見えているところだけの放射輝度を反映するGと、投影を表す内積を組み込むと、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { 1 }{ \cos { \theta _{ o } } } \int _{ M }^{ }{ L\left( \omega _{ o },p_{ m } \right) G_1\left( \omega _{ o },p_{ m } \right) \left< \omega _{ o },\omega _{ m } \right> dp_{ m } } }$

これを統計ベース(Statistical)の方程式にもっていけば、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { 1 }{ \cos { \theta _{ o } } } \int _{ \Omega }^{ }{ L\left( \omega _{ o },\omega_{ m } \right) G_1\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } }$

だいぶ扱いやすい式になってきました。ここでさらにL以外をまとめ上げ、ここに "distribution of visible normals" (可視法線分布）と名前を付けます。

$\displaystyle { D_{ \omega }\left( \omega _{ m } \right) =\frac { G_1\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) }{ \cos { \theta _{ o } } } }$

すると先の式はそれに伴って、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { 1 }{ \cos { \theta _{ o } } } \int _{ \Omega }^{ }{ L\left( \omega _{ o },\omega_{ m } \right) G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ L\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ L\left( \omega _{ o },\omega_{ m } \right) D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } }$

こうすると、出射放射輝度はこの"distribution of visible normals" (可視法線分布）に重みづけされた平均であるという見方ができます。なにやらこじつけで無理やり名前を付けたようにも見えなくありませんが、"distribution "（分布）というからには、この新しい $D_{\omega}$ はちゃんと正規化されています。それはつまり、

$\displaystyle { \int _{ \Omega }^{ }{ D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } =1 }$

という意味です。だからこそ"出射放射輝度は可視法線分布により重みづけされた平均だ"という捉え方は、的を射ているといえます。これは以下のように確認することができます。

$\displaystyle { \int _{ \Omega }^{ }{ D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } =\int _{ \Omega }^{ }{ \frac { G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) }{ \cos { \theta _{ o } } } d\omega _{ m } } \\ =\frac { 1 }{ \cos { \theta _{ o } } } \int _{ \Omega }^{ }{ G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\frac { \int _{ \Omega }^{ }{ G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } }{ \int _{ \Omega }^{ }{ G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } } \\ =1 }$

マイクロBRDF

今まではマイクロサーフェスからの放射輝度だけを考えてきました。ただ実際にはマイクロサーフェスもなんらかの反射特性を有しており、入射と出射にはやはりその性質を考える必要があります。そこで、マイクロサーフェスのそれぞれの微小面のミクロの世界のBRDFを以下のように名前を付けることにします。

$\displaystyle { \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) }$

すると、微小面からの出射放射輝度は、レンダリング方程式から、

$\displaystyle { L\left( \omega _{ o },\omega _{ m } \right) =\int _{ \Omega _{ i } }^{ }{ \frac { dL\left( \omega _{ o },\omega _{ m } \right) }{ d\omega _{ i } } d\omega _{ i } } \\ L\left( \omega _{ o },\omega _{ m } \right) =\int _{ \Omega _{ i } }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> L\left( \omega _{ i } \right) d\omega _{ i } } }$

マクロな世界、マイクロサーフェスの出射放射輝度は、可視法線分布に重みづけされた平均だったので、

$\displaystyle { L\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ L\left( \omega _{ o },\omega _{ m } \right) D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } }$

ここで微小立体角の入射あたりの出射放射輝度の寄与を考えてみます

$\displaystyle { dL\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ dL\left( \omega _{ o },\omega _{ m } \right) D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } }$

これはやはり微小面からの出射放射輝度を考えればいいので、

$\displaystyle { dL\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> L\left( \omega _{ i } \right) D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } \\ =L\left( \omega _{ i } \right) \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } }$

これを一度積分形式に戻ると、

$\displaystyle { L\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \left( \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } \right) d\omega _{ m } } }$

となり、さらにマクロBRDF ( $\rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right)$ ) は一般に、

$\displaystyle { L\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \cos { \theta _{ i } } d\omega _{ m } } }$

であることを考え、 $D_\omega$ を展開しながら整理すると、

$\displaystyle { L\left( \omega _{ i } \right) \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \cos { \theta _{ i } } =L\left( \omega _{ i } \right) \left( \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } \right) \\ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \cos { \theta _{ i } } =\int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } \\ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { 1 }{ \cos { \theta _{ i } } } \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } \\ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { 1 }{ \cos { \theta _{ i } } } \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> \frac { G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) }{ \cos { \theta _{ o } } } d\omega _{ m } } \\ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { 1 }{ \cos { \theta _{ i } } \cos { \theta _{ o } } } \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } }$

と整理でき、またついでに内積を使った表現では、

とすることもできますね。だいぶBRDFの詳細が見えてきました。

抜け落ちた遮蔽

先の節で、定式化ができたように感じてしまいますが、抜け落ちてしまっているところがあります。一つは $G_1 \left( \omega_o, \omega_m \right)$ です。ここではoなので、出ていくときの遮蔽を考慮に入れています。しかしながら入射はどうか？というと考慮できていません。これはoをiにしても同様の問題が起きます。つまるところ実際には両方の遮蔽を考慮しないと変なわけです。これについてはいったんメモでとどめ、後ほど再び議論します。

マイクロBRDF

Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" では、マイクロBRDFを二つのケースを紹介しています。一つは完全拡散面、もう一つは完全鏡面です。ここでは完全鏡面を仮定して、BRDFを具体化していきます。

完全鏡面を表現するのにはやはりデルタ関数を使ってモデル化するのが良さそうです。例えば試しに完全鏡面のBRDFを考えるとき、直感的に、二つのベクトルが完全に反射の関係性を満たすところにピークのあるデルタ関数 $\delta \left( \omega _{ h },\omega _{ n } \right)$ をそのまま使ってみますと、

$\displaystyle { \rho _{ mirror }\left( \omega _{ o },\omega _{ i },\omega _{ n } \right) =\delta \left( \frac { \omega _{ o }+\omega _{ i } }{ \left\| \omega _{ o }+\omega _{ i } \right\| } ,\omega _{ n } \right) =\delta \left( \omega _{ h },\omega _{ n } \right) }$

しかし、実はこれは問題があり、レンダリング方程式に入れてみると、

$\displaystyle { L_{ o }=\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \rho _{ mirror }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \cos { \theta _{ i } } d\omega _{ i } } \\ =\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \delta \left( \omega _{ h },\omega _{ n } \right) \cos { \theta _{ i } } d\omega _{ i } } \\ =L\left( \omega _{ reflect } \right) \cos { \theta _{ i } } }$

これは見るからにおかしいです。つまり正しくはデルタ関数をそのまま使うのではなく、なんらかの補正係数が必要だったわけです。したがって、正しくは以下のように補正項をつけます。

$\displaystyle { \rho _{ mirror }\left( \omega _{ o },\omega _{ i },\omega _{ n } \right) =\frac { \delta \left( \omega _{ h },\omega _{ n } \right) }{ \cos { \theta _{ i } } } \\ L_{ o }=\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \rho _{ mirror }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \cos { \theta _{ i } } d\omega _{ i } } \\ =\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \frac { \delta \left( \omega _{ h },\omega _{ n } \right) }{ \cos { \theta _{ i } } } \cos { \theta _{ i } } d\omega _{ i } } \\ =\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \delta \left( \omega _{ h },\omega _{ n } \right) d\omega _{ i } } \\ =L\left( \omega _{ reflect } \right) }$

これを踏まえ、先の式でマイクロBRDFはどのようになるのかを考えてみたいです。

$\displaystyle { \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { 1 }{ \left< \omega _{ i },\omega _{ g } \right> \left< \omega _{ i },\omega _{ g } \right> } \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } }$

しかし補正係数は今回自明ではないため、いったん k と置くことにします。

$\displaystyle { \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =k\delta \left( \omega _{ h },\omega _{ m } \right) }$

マイクロサーフェスとはいえ、通常のBRDFやBSDFと同様に、エネルギーは完全に保存されるはずなので、以下が成り立つはずです。

$\displaystyle { \int _{ \Omega _{ i } }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left| \omega _{ i }\cdot \omega _{ m } \right| d\omega _{ i } } =1\\ \int _{ \Omega _{ i } }^{ }{ k\delta \left( \omega _{ h },\delta \left( \omega _{ h } \right) \right) \left| \omega _{ i }\cdot \omega _{ m } \right| d\omega _{ i } } =1 }$

しかし困ったことに、デルタ関数の引数である $\omega _{ h }$ は積分の変数そのままではありません。したがって積分結果はいくばくかの補正がかかります。デルタ関数の引数に補正がかからないように変数変換を行いたくなってきます。

変数変換

先の要求を改めて確認すると、 $\omega _{ h }$ と、 $\omega _{ i }$ , $\omega _{ o }$ とを自由に変換できるようになりたい、というものでした。これには幾何学的関係性を考えることで係数が見えてきます。※ Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces"

まずは記号を整理します。

$\displaystyle { \vec { h } =\vec { i } +\vec { o } \\ \vec { h_{ r } } =\frac { \vec { h } }{ \left\| \vec { h } \right\| } }$

これはイメージとしては、

f:id:ushiostarfish:20180325181358p:plain

というようなかんじです。次に並べ替えて、

f:id:ushiostarfish:20180325181523p:plain

さらにハーフベクトルを書き込むと、

f:id:ushiostarfish:20180325181646p:plain

ここで、立体角 $\Delta \omega h$ と $\Delta \omega o$ の微小な関係性は、

$\displaystyle { \Delta \omega h=\left| \vec { o } \cdot \vec { h_{ r } } \right| \Delta \omega o }$

であり、さらに、

f:id:ushiostarfish:20180325182044p:plain

立体角 $\Delta \omega h_r$ と $\Delta \omega o$ の微小な関係性は、

$\displaystyle { \Delta \omega h_{ r }=\frac { \left| \vec { o } \cdot \vec { h_{ r } } \right| }{ { \left\| \vec { h } \right\| }^{ 2 } } \Delta \omega o }$

となり、さらに、hの長さを iとo、そしてhrを使って表すのをとっかかりにして、

$\displaystyle { \left\| \vec { h } \right\| =\left| \left( \vec { i } +\vec { o } \right) \cdot \vec { h_{ r } } \right| \\ =\left| \vec { i } \cdot \vec { h_{ r } } +\vec { o } \cdot \vec { h_{ r } } \right| \\ =\left| 2\vec { i } \cdot \vec { h_{ r } } \right| =\left| 2\vec { o } \cdot \vec { h_{ r } } \right| }$

となることから、

$\displaystyle { { \left\| \vec { h } \right\| }^{ 2 }={ \left| 2\vec { o } \cdot \vec { h_{ r } } \right| }^{ 2 }=4{ \left| \vec { o } \cdot \vec { h_{ r } } \right| }^{ 2 } }$

これを使って、

$\displaystyle { \Delta \omega h_{ r }=\frac { \left| \vec { o } \cdot \vec { h_{ r } } \right| }{ 4{ \left| \vec { o } \cdot \vec { h_{ r } } \right| }^{ 2 } } \Delta \omega o\\ \Delta \omega h_{ r }=\frac { 1 }{ 4\left| \vec { o } \cdot \vec { h_{ r } } \right| } \Delta \omega o }$

となるほど巧妙にも、幾何学的関係が明らかになりました。論文中ではヤコビアンの表記として以下のように表現されています。

$\displaystyle { \left\| \frac { \omega h_{ r } }{ \omega o } \right\| =\frac { 1 }{ 4\left| \vec { o } \cdot \vec { h_{ r } } \right| } }$

また屈折の場合も似たような感じで、以下のようにhを表して、微小な関係性を導くことができます。（※スネルの法則から屈折ベクトルの関係性を満たしていることを確認できます）

$\displaystyle { \vec { h } =-\eta _{ 1 }\vec { i } -\eta _{ 2 }\vec { o } }$

ただ今回は長くなってしまうのでいったんこの辺で割愛します。気になる方は、Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces" を直接参照していただけると良いと思います。

マイクロBRDF その2

さて、変数変換ができるようになったので、先の式、

を変数変換すると、

$\displaystyle { \int _{ \Omega _{ m } }^{ }{ k\delta \left( \omega _{ h },\delta \left( \omega _{ h } \right) \right) \left| \omega _{ i }\cdot \omega _{ m } \right| 4\left| \omega _{ i }\cdot \omega _{ h } \right| d\omega _{ m } } =1\\ \int _{ \Omega _{ m } }^{ }{ \delta \left( \omega _{ h },\delta \left( \omega _{ h } \right) \right) k4{ \left| \omega _{ i }\cdot \omega _{ h } \right| }^{ 2 }d\omega _{ m } } =1 }$

となり、mとhが一致しているので、簡単にデルタ関数を外すことができます。したがって、これを満たすkは、

$\displaystyle { k4{ \left| \omega _{ i }\cdot \omega _{ h } \right| }^{ 2 }=1\\ k=\frac { 1 }{ 4{ \left| \omega _{ i }\cdot \omega _{ h } \right| }^{ 2 } } }$

と求めることができ、さらにフレネル項を考慮してあげたマイクロBRDFは、以下のようになります。

$\displaystyle { \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\left\| \frac { \omega h }{ \omega i } \right\| \frac { F\left( \omega _{ o },\omega _{ h } \right) \delta \left( \omega _{ h },\omega _{ m } \right) }{ \left| \omega _{ i }\cdot \omega _{ h } \right| } =\frac { F\left( \omega _{ o },\omega _{ h } \right) \delta \left( \omega _{ h },\omega _{ m } \right) }{ 4{ \left| \omega _{ i }\cdot \omega _{ h } \right| }^{ 2 } } }$

これを先のマクロBRDFの式に代入して、hとmは同じものを表していることに注意しつつ整理すると、

$\displaystyle { \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { 1 }{ \left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\frac { 1 }{ \left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \int _{ \Omega }^{ }{ \frac { F\left( \omega _{ o },\omega _{ h } \right) \delta \left( \omega _{ h },\omega _{ m } \right) }{ 4{ \left| \omega _{ i }\cdot \omega _{ h } \right| }^{ 2 } } \left< \omega _{ i },\omega _{ m } \right> G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\frac { 1 }{ \left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \int _{ \Omega }^{ }{ \frac { F\left( \omega _{ o },\omega _{ h } \right) \delta \left( \omega _{ h },\omega _{ m } \right) }{ 4 } G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\frac { 1 }{ \left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \int _{ \Omega }^{ }{ \delta \left( \omega _{ h },\omega _{ m } \right) \frac { F\left( \omega _{ o },\omega _{ h } \right) G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) D\left( \omega _{ m } \right) }{ 4 } d\omega _{ m } } \\ =\frac { 1 }{ \left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \frac { F\left( \omega _{ o },\omega _{ h } \right) G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) D\left( \omega _{ m } \right) }{ 4 } \\ =\frac { F\left( \omega _{ o },\omega _{ h } \right) G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) D\left( \omega _{ m } \right) }{ 4\left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } }$

これが、良く知られたマイクロファセットベースのBRDFの形式です。(※Gが片側しか考慮していないことを除けば）

エネルギー保存とマスキング関数

BRDF, BSDFなどのエネルギー保存として以下の式がよく提示されます。

$\displaystyle { \int _{ \Omega _{ o } }^{ }{ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left| \omega _{ o }\cdot \omega _{ g } \right| d\omega _{ o } } \le 1\forall \omega _{ i } }$

完全にエネルギーが保存される場合は、

$\displaystyle { \int _{ \Omega _{ o } }^{ }{ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left| \omega _{ o }\cdot \omega _{ g } \right| d\omega _{ o } } = 1\forall \omega _{ i } }$

これはなんだったかといえば、例えば放射照度1が観測されたとして、その時の放射発散度を積分で求めていると解釈することができ、それはやはり同じく1である、というふうに考えると自然です。

そしてここでヘルムホルツ（Helmoholtz）の相反性を考えると、やはりiとoを逆転されても成り立つはずで、

$\displaystyle { \int _{ \Omega _{ i } }^{ }{ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left| \omega _{ i }\cdot \omega _{ g } \right| d\omega _{ i } } =1\forall \omega _{ o } }$

とも良く書かれます。これは見方を変えると、全方位で周囲から来る放射輝度が1であったとき、どの方向への出射放射輝度も1である、という解釈ができます。この性質を数値積分によって確かめるテストを、"White Furnace Test"と呼びます。

では先のBRDFはどうか？というのを考えてみると、フレネル項を除けば、満たすことができます。なぜなら表面はマイクロサーフェスは完全鏡面を仮定しており、吸収されることははなから前提に存在しないためです。

$\displaystyle { \int _{ \Omega _{ i } }^{ }{ \frac { G_{ 1 }\left( \omega _{ h },\omega _{ o } \right) D\left( \omega _{ h } \right) }{ 4\left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \left| \omega _{ i }\cdot \omega _{ g } \right| d\omega _{ i } } =1\forall \omega _{ o }\\ \int _{ \Omega _{ i } }^{ }{ \frac { G_{ 1 }\left( \omega _{ h },\omega _{ o } \right) D\left( \omega _{ h } \right) }{ 4\left| \omega _{ o },\omega _{ g } \right| } d\omega _{ i } } =1\forall \omega _{ o } }$

しかし、これはちょうど以下の図のような状況です。

f:id:ushiostarfish:20180325221717p:plain ※ Figure 6. (b) Normalization of specular microfacet-based BRDFs. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

もしかすると、iとoを逆にしたほうが図としっくりくるかもしれません。

$\displaystyle { \int _{ \Omega _{ o } }^{ }{ \frac { G_{ 1 }\left( \omega _{ h },\omega _{ i } \right) D\left( \omega _{ h } \right) }{ 4\left| \omega _{ i },\omega _{ g } \right| } d\omega _{ o } } =1\forall \omega _{ i } }$

図では完全にマイクロサーフェス上をエネルギーが突き抜けてしまっています。これはなぜかといえば、単方向しか遮蔽を考慮できておらず、最後の式では出射に対して遮蔽がありません。そこで両方向遮蔽を考慮した $G_2$ が都合よく見つかったと仮定して考えてみましょう。

$\displaystyle { \int _{ \Omega _{ o } }^{ }{ \frac { G_{ 2 }\left( \omega _{ h },\omega _{ i },\omega _{ o } \right) D\left( \omega _{ h } \right) }{ 4\left| \omega _{ i },\omega _{ g } \right| } d\omega _{ o } } }$

・・・これは当然ですがエネルギーが失われます。

これを表しているのが以下の図です。

f:id:ushiostarfish:20180325223603p:plain ※ Figure 6. (c) Normalization of specular microfacet-based BRDFs. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

しかしマイクロサーフェス上は完全鏡面を仮定したにもかかわらず、エネルギーが失われることは、極めて不自然です。なぜエネルギーが失われたかといえば、遮蔽された部分を0にしているからで、本来なら遮蔽されたとしても、そこからまた反射を繰り返し、どこかでは必ず外へ出ていくはずです。これは多重拡散をなんらかの形で考慮しなければ、エネルギーを保存させることが難しいことを示唆しています。これを表したのが以下の図です。

f:id:ushiostarfish:20180325224114p:plain ※ Figure 6. (d) Normalization of specular microfacet-based BRDFs. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" ではこれに対する解決策は提示されていませんが、しかし後の 2016年に、

Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-scattering microfacet BSDFs with the Smith model"

の論文が発表され、この多重拡散部分も解析的にモデル化することに成功しています。

f:id:ushiostarfish:20180325224649p:plain Figure 16: White furnace test for different microfacet materials. Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-scattering microfacet BSDFs with the Smith model" より

こちらは完全に本稿の範囲を超えてしまう上、自分のレベルではまだ理解できていないため、紹介にとどめることにいたします。

話を戻しますが、遮蔽を一部無視する形であれ、不完全でありながらもエネルギーの保存を確認することのできる、

のテストはそれなりに便利であり、これを論文中では、"Weak White Furnace Test"と呼んでいます。ただし、これは片方向での遮蔽のみでBRDFを設計することを勧めているわけではないことは注意が必要です。

Gの中身, Smithモデル

今までGの中身についてはあまり議論してきませんでした。枠組みがだいぶできてきたので、そろそろ中身に踏み込んでいきます。マスキング関数は一意に定まるか？の節で、Gを考えるときには、なんらかの仮定が必要という話をしました。スミスモデルの重要な仮定は、

・ミクロな表面の高さと向きは、無相関である

というところです。以下の図の右のような状態です。

f:id:ushiostarfish:20180331193214p:plain Figure 7. Microsurfaces and their autocorrelation functions. (left) A real-world continuous microsurface with large autocorrelation distance. (right) A uncorrelated surface, where each microfacet is not correlated to its neighborhood, as Smith models. Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-scattering microfacet BSDFs with the Smith model" より

なんだかそんな表面あり得るのか？という気もしないでもありませんが、このおかげで G を以下のように二つの関数に分離することができます。

$\displaystyle { G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) =G_{ 1 }^{ local }\left( \omega _{ o },\omega _{ m } \right) G_{ 1 }^{ dist }\left( \omega _{ o } \right) }$

$G_{ 1 }^{ local }\left( \omega _{ o },\omega _{ m } \right)$ は、出射に対して表面が見えているか？という角度に対する関数で、 $G_{ 1 }^{ dist }\left( \omega _{ o } \right)$ は、別の表面にどの程度遮蔽されているか？という関数です。こちらは遮蔽ですので、どうやらミクロな表面の高さ分布によって決まりそうです。

なぜ分離できるんでしょうか？例えば、ミクロな表面の高さと角度になんらかの関係性があり、例えば以下のような分布をしているとします。

f:id:ushiostarfish:20180331201915p:plain

ちょうど条件付き確率のような構造です。これでは、例えば高さ h > 3 であり、かつ 60 <= θ <= 90 であるミクロサーフェスが全体のどの程度を占めるのかを考えたいとき、 hに依存してθの分布を考えたりなど、相互の関係性を考慮にいれなければ、正しく求められません。しかし仮に相互に相関がない場合は、例えば以下のような図の状態です。

f:id:ushiostarfish:20180331201847p:plain

完全に格子状になっていますね、これなら、例えば高さ h > 3 であり、かつ 60 <= θ <= 90 であるミクロサーフェスが全体のどの程度を占めるのか？は、個別に関数を考えて、その積で表すことができる、ということです。

中身の話に移ると、まず、 $G_{ 1 }^{ local }\left( \omega _{ o },\omega _{ m } \right)$ は "local masking function" と呼ばれ、出射に対して表面が見えているか？という関数だったので、

$\displaystyle { G_{ 1 }^{ local }\left( \omega _{ o },\omega _{ m } \right) =\chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) }$

で表されます。ここで $\chi^+ \left( x \right)$ は、ヘヴィサイドの階段関数であり、以下のような関数です

f:id:ushiostarfish:20180331203305p:plain

※ ヘヴィサイドの階段関数 - Wikipedia より

平たい話、出射に対して表面が見えていれば 1 ,裏返って見えていなければ0 というわけです。

では、 $G_{ 1 }^{ dist }\left( \omega _{ o } \right)$ は、別の表面にどの程度遮蔽されているか？という関数だと述べましたが、この関数は未知の関数です。しかしながら、出射方向の投射面積で述べた、投影面積の関係式、

に Gの具体的な形を代入してみると、

$\displaystyle { \cos { \theta _{ o } } =\int _{ \Omega }^{ }{ G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ G_{ 1 }^{ local }\left( \omega _{ o },\omega _{ m } \right) G_{ 1 }^{ dist }\left( \omega _{ o } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) G_{ 1 }^{ dist }\left( \omega _{ o } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =G_{ 1 }^{ dist }\left( \omega _{ o } \right) \int _{ \Omega }^{ }{ \chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ G_{ 1 }^{ dist }\left( \omega _{ o } \right) =\frac { \cos { \theta _{ o } } }{ \int _{ \Omega }^{ }{ \chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } } }$

と導かれ、したがって、

$\displaystyle { G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) =\chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) \frac { \cos { \theta _{ o } } }{ \int _{ \Omega }^{ }{ \chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } } }$

と、Dの具体的な形が定まれば、Gは確かに自動的に定まるようになりました。ただ実際これをBRDFなどで使おうと思うと、解析的に式内の積分が解けないケースでは、評価のたびにこの積分を数値的に評価をしなければならず、非効率です。そのため事前計算を行い、テーブルに格納しておくなどの工夫を余儀なくされます。そこで、次のパートでは、現在広く使われている、SmithモデルではGをどのように扱っているのか？を考えていきます。

Smithモデルの導出

Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces" および、Earl Hammon, Jr, GDC, "PBR Diffuse Lighting for GGX+Smith Microsurfaces" の151ページ~157ページによると、Smithモデルにおいては、ミクロな表面からの光線を追跡する考え方で、Gを求める方法が紹介されています。

以下の図が概念図です。 f:id:ushiostarfish:20180331205923p:plain

※Figure 16: Geometry for Smith shadowing-masking G1 for direction v, corresponding to a visibility ray has starting height ξ0 and slope μ. At distance τ (measured along macrosurface), the microsurface has height ξ and slope q. Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces"より ※ 概念図であるため、ミクロな表面はつながって描かれています。 ※ 概念図は一次元的ですが、等方的なDを考える場合はどのように１次元に切り取っても同じであるため、一次元で考えます。

大変ごちゃごちゃしていますが、あるミクロ表面の高さ $\xi_0$ の場所から角度 $\theta _v$ の角度で横方向に $\tau$ だけ進んでいる状況で、その時のミクロ表面の高さが $\xi$ であり、さらにもうちょっと $\Delta \tau$ だけ進むところの図です。 $q$ は、横方向に $\tau$ 進んだときのミクロ表面の勾配で、 $\mu$ は光線の勾配です。

もうちょっと $\Delta \tau$ だけ進む、という状況について考えてみます。

$\mu$ については、 $\theta_v$ から、

$\displaystyle { \mu =\left| \tan { \left( \frac { \pi }{ 2 } -\theta _{ v } \right) } \right| =\left| \frac { 1 }{ \tan { \theta _{ v } } } \right| =\left| \cot \theta _{ v } \right| }$

となります。絶対値がついているのは、θのマイナスを考慮しているためです。

次に、ちょっと $\Delta \tau$ だけ進んだときにミクロ表面に衝突するための条件は、高さに着目して、進む前にぶつかっていない、つまり、

$\displaystyle { \xi _{ 0 }+\mu \tau >\xi }$

であり、かつ進んだときにぶつかる、

$\displaystyle { \xi _{ 0 }+\mu \tau +\mu \Delta \tau <\xi +q\Delta }$

※Earl Hammon, Jr, GDC, "PBR Diffuse Lighting for GGX+Smith Microsurfaces" では、この式の不等号の向きが逆です。これはタイポだと思われます。

この二つの条件が必要であり、二つ目の式を整理すると、

$\displaystyle { \xi _{ 0 }+\mu \tau +\mu \Delta \tau <\xi +q\Delta \tau \\ \xi _{ 0 }+\mu \tau +\mu \Delta \tau -q\Delta \tau <\xi \\ \xi >\xi _{ 0 }+\mu \tau +\mu \Delta \tau -q\Delta \tau }$

となり、二つをくっつけると、

$\displaystyle { \xi _{ 0 }+\mu \tau >\xi >\xi _{ 0 }+\mu \tau +\mu \Delta \tau -q\Delta \tau \\ \xi _{ 0 }+\mu \tau >\xi >\xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }$

このことから、

$\displaystyle { -\left( q-\mu \right) \Delta \tau <0\\ -\left( q-\mu \right) <0\\ q-\mu >0\\ q>\mu }$

であることがわかります。これが、ちょっと $\Delta \tau$ だけ進んだときにミクロ表面に衝突するための条件、ということになります。

ここで高さ分布を表す関数を、

$\displaystyle { P_{ 1 }\left( h \right) }$

で表し、そしてこれは、分布なので、

$\displaystyle { \int _{ -\infty }^{ \infty }{ P_{ 1 }\left( h \right) dh } =1 }$

であります。また、単一方向へ（一次元の）の勾配分布関数を、

$\displaystyle { P_{ 2 }\left( q \right) }$

で表し、これは何かといえば、引数に $\tan \theta$ を入れると、ミクロ表面に $\theta$ を持つ分布が返ってくるという関数です。尺度が勾配であるだけで、実際にはDから機械的に求めます。その詳細はいったん省略しますが、後に詳しく議論します。この関数は既知である、ということを前提にして次に進みます。なぜこんな関数が必要なのかというと、先の概念図でのq をうまく扱うため、と言ってもよいかもしれません。

こちらも分布なので、

$\displaystyle { \int _{ \infty }^{ \infty }{ P_{ 2 }\left( q \right) dq } =1 }$

であり、さらに例えば、

$\displaystyle { -\theta \le q\le \theta }$

の範囲に角度をもつミクロな表面の全体からみた割合は、

$\displaystyle { \int _{ \tan { \left( -\theta \right) } }^{ \tan { \theta } }{ P_{ 2 }\left( q \right) dq } }$

で求められる、というわけです。

これを踏まえて、ちょっと $\Delta \tau$ だけ進んだときにミクロ表面に衝突する条件、

$\displaystyle { \xi _{ 0 }+\mu \tau >\xi >\xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }$

および、

$\displaystyle { q>\mu }$

から、ちょっと $\Delta \tau$ だけ進んだときにミクロ表面に衝突する確率は、この条件を満たすミクロ表面の割合と一致するはずです。したがって、その確率は、

$\displaystyle { \int _{ \mu }^{ \infty }{ \int _{ \xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) P_{ 2 }\left( q \right) dhdq } } \\ =\int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \int _{ \xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dhdq } } }$

ここで極限をとります。

$\displaystyle { \lim _{ \Delta \tau \rightarrow d\tau }{ \Delta \tau } =d\tau }$

すると右の部分は、

$\displaystyle { \lim _{ \Delta \tau \rightarrow d\tau }{ \int _{ \xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dh } } =P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \left\{ \left( \xi _{ 0 }+\mu \tau \right) -\left( \xi _{ 0 }+\mu \tau -\left( q-\mu \right) d\tau \right) \right\} \\ =P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \left( q-\mu \right) d\tau }$

したがって、確率は、

$\displaystyle { \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \int _{ \xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dhdq } } =\int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \left( q-\mu \right) d\tau dq } \\ =d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }$

となります。しかし、このアイディアには抜けていることがあります。今までの議論は、暗黙に、 $\tau$ 進んだ時点で、高さ $\xi _{ 0 }+\mu \tau$ 以下にあらかじめ存在していなければならない点です。これは条件付き確率として考えることができ、Aの条件のもとBが起こる確率は、

$\displaystyle { P\left( B|A \right) =\frac { P\left( B\wedge A \right) }{ P\left( A \right) } }$

と表されます。先ほどまで考えていた、確率というのは、 $P\left( B\wedge A \right)$ の部分に相当するため、

$\displaystyle { P\left( A\wedge B \right) =d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }$

となり、 $P\left( A \right)$ は、

$\displaystyle { P\left( A \right) =\int _{ -\infty }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dh } }$

これをいったん $f$ とおきますと、

$\displaystyle { \int _{ -\infty }^{ x }{ P_{ 1 }\left( h \right) dh } =f\left( x \right) \\ \int _{ -\infty }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dh } =f\left( \xi _{ 0 }+\mu \tau \right) }$

すると、 $d\tau$ だけ進んだときにミクロ表面に衝突する確率は、

$\displaystyle { P\left( A|B \right) =\frac { d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }{ \int _{ -\infty }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dh } } \\ =\frac { d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }{ f\left( \xi _{ 0 }+\mu \tau \right) } }$

となるわけです。ようやく少し見えてはきましたが、あくまで $d\tau$ の増加分に対する衝突確率でした。これをなんとかして、ある $\xi$ から傾き $\mu$ で $\tau$ 進んだときの生き残り割合として以下のような関数に定式化したいと考えます。

$\displaystyle { S\left( \xi ,\mu ,\tau \right) }$

この関数は、 $\tau$ が進めば進むほど生き残る確率は下がっていきます。これを単純化して、 $x_0, x_1,...$ をステップごとの生存確率だとすると、何回かステップを進めたときの生存確率は、

$\displaystyle { S_{ 1 }=x_{ 1 }\\ S_{ 2 }=x_{ 2 }x_{ 1 }\\ S_{ 3 }=x_{ 3 }x_{ 2 }x_{ 1 }\\ S_{ 4 }=x_{ 4 }x_{ 3 }x_{ 2 }x_{ 1 } }$

のように１ステップごとの生存確率の積で表せます。ここで４ステップ目進めるときの部分に着目すると、

$\displaystyle { \Delta S_{ 4 }=S_{ 4 }-S_{ 3 }\\ =x_{ 4 }x_{ 3 }x_{ 2 }x_{ 1 }-x_{ 3 }x_{ 2 }x_{ 1 }\\ =x_{ 4 }S_{ 3 }-S_{ 3 } }$

これを任意の１ステップに抽象化して、

$\displaystyle { \Delta S_{ n }=x_{ n }S_{ n-1 }-S_{ n-1 }\\ \Delta S_{ n }=S_{ n-1 }\left( x_{ n }-1 \right) }$

ここで $x_n$ は、1-衝突確率であるので、

$\displaystyle { \Delta S_{ n }=S_{ n-1 }\left( 1-P_{ collision }-1 \right) \\ \Delta S_{ n }=-S_{ n-1 }P_{ collision } }$

結果衝突せずに生き残る確率の変化量は、最終的に、

$\displaystyle { dS=-\left( \frac { d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }{ f\left( \xi _{ 0 }+\mu \tau \right) } \right) S\\ \frac { dS }{ d\tau } =-\left( \frac { d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }{ f\left( \xi _{ 0 }+\mu \tau \right) } \right) S }$

となり、微分方程式の形でSを表すことができました。こうなると解きたくなってきます。いったん長いので、

$\displaystyle { g\left( \tau \right) =\frac { P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }{ f\left( \xi _{ 0 }+\mu \tau \right) } }$

と置くことにして、

$\displaystyle { \\ \dot { S } \left( x \right) =-g\left( x \right) S\left( x \right) \\ \frac { \dot { S } \left( x \right) }{ S\left( x \right) } =-g\left( x \right) \\ \int { \frac { \dot { S } \left( x \right) }{ S\left( x \right) } dx } =\int { -g\left( x \right) dx } +C }$

置換積分を実行して、

$\displaystyle { S\left( x \right) =y\\ \dot { S } \left( x \right) =\frac { dy }{ dx } \\ \dot { S } \left( x \right) dx=dy\\ dx=\frac { dy }{ \dot { S } \left( x \right) } \\ \int { \frac { 1 }{ y } dy } =\int { -g\left( x \right) dx } +C\\ \ln { \left( y \right) } =\int { -g\left( x \right) dx } +C\\ { e }^{ \int { -g\left( x \right) dx } +C }=y\\ { e }^{ \int { -g\left( x \right) dx } +C }=S\\ { e }^{ \int _{ 0 }^{ \tau }{ -g\left( x \right) dx } +C }=S\left( \tau \right) }$

積分定数は、

$\displaystyle { S\left( 0 \right) =1\\ { e }^{ C }=1\\ C=0 }$

したがって、

$\displaystyle { { e }^{ \int _{ 0 }^{ \tau }{ -g\left( x \right) dx } }=S\left( \tau \right) }$

ここで、gの積分をさらに考えていきます。

まず、

$\displaystyle { f\left( \xi _{ 0 }+\mu \tau \right) =\int _{ -\infty }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dh } }$

に見やすく名前をつけて、

$\displaystyle { f\left( \xi _{ 0 }+\mu \tau \right) =f_{ \tau }\left( \tau \right) }$

これの微分は、

$\displaystyle { \dot { f_{ \tau } } \left( \tau \right) =\frac { d }{ d\tau } f\left( \xi _{ 0 }+\mu \tau \right) =\mu P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) }$

ここで、今筆者と読者に天啓が下ったとして、

$\displaystyle { \Lambda \left( \mu \right) =\frac { 1 }{ \mu } \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }$

と置くと、

$\displaystyle { g\left( \tau \right) =\Lambda \left( \mu \right) \frac { \dot { f_{ \tau } } \left( \tau \right) }{ f_{ \tau }\left( \tau \right) } }$

となり、積分は、

$\displaystyle { \int _{ 0 }^{ \tau }{ g\left( t \right) d } t=\int _{ 0 }^{ \tau }{ \Lambda \left( \mu \right) \frac { \dot { f_{ \tau } } \left( t \right) }{ f_{ \tau }\left( t \right) } dt } }$

さらに置換積分で、

$\displaystyle { y=f_{ \tau }\left( t \right) \\ \frac { dy }{ dt } =\dot { f_{ \tau } } \left( t \right) \\ dy=dt\dot { f_{ \tau } } \left( t \right) \\ \frac { dy }{ \dot { f_{ \tau } } \left( t \right) } =dt\\ =\int _{ f_{ \tau }\left( 0 \right) }^{ f_{ \tau }\left( t \right) }{ \Lambda \left( \mu \right) \frac { 1 }{ y } dy } }$

あとは素直に、

$\displaystyle { =\left[ \Lambda \left( \mu \right) \ln { \left| y \right| } \right] ^{ f_{ \tau }\left( t \right) }_{ f_{ \tau }\left( 0 \right) }\\ =\left[ \Lambda \left( \mu \right) \ln { \left( y \right) } \right] ^{ f_{ \tau }\left( t \right) }_{ f_{ \tau }\left( 0 \right) }\\ =\Lambda \left( \mu \right) \ln { \left( f_{ \tau }\left( \tau \right) \right) } -\Lambda \left( \mu \right) \ln { \left( f_{ \tau }\left( 0 \right) \right) } \\ =\Lambda \left( \mu \right) \left\{ \ln { \left( f_{ \tau }\left( \tau \right) \right) } -\ln { \left( f_{ \tau }\left( 0 \right) \right) } \right\} \\ =\Lambda \left( \mu \right) \left\{ \ln { \left( f\left( \xi _{ 0 }+\mu \tau \right) \right) } -\ln { \left( f\left( \xi _{ 0 } \right) \right) } \right\} \\ =\Lambda \left( \mu \right) \ln { \left( \frac { f\left( \xi _{ 0 }+\mu \tau \right) }{ f\left( \xi _{ 0 } \right) } \right) } }$

以上をまとめると、

$\displaystyle { S\left( \xi _{ 0 },\mu ,\tau \right) ={ e }^{ \int _{ 0 }^{ \tau }{ -g\left( x \right) dx } }\\ ={ e }^{ -\Lambda \left( \mu \right) \ln { \left( \frac { f\left( \xi _{ 0 }+\mu \tau \right) }{ f\left( \xi _{ 0 } \right) } \right) } }\\ ={ \left( { e }^{ \ln { \left( \frac { f\left( \xi _{ 0 }+\mu \tau \right) }{ f\left( \xi _{ 0 } \right) } \right) } } \right) }^{ -\Lambda \left( \mu \right) }\\ ={ \left( \frac { f\left( \xi _{ 0 }+\mu \tau \right) }{ f\left( \xi _{ 0 } \right) } \right) }^{ -\Lambda \left( \mu \right) }\\ ={ \left( \frac { f\left( \xi _{ 0 } \right) }{ f\left( \xi _{ 0 }+\mu \tau \right) } \right) }^{ \Lambda \left( \mu \right) } }$

ただ実際には、 $\tau$ は、∞になるべき存在です。そこで、生存確率は、

$\displaystyle { S\left( \xi _{ 0 },\mu ,\tau \right) ={ \left( \frac { f\left( \xi _{ 0 } \right) }{ f\left( \xi _{ 0 }+\mu \tau \right) } \right) }^{ \Lambda \left( \mu \right) }\\ S\left( \xi _{ 0 },\mu \right) =\lim _{ \tau \rightarrow \infty }{ S\left( \xi _{ 0 },\mu ,\tau \right) } \\ ={ \left( \frac { f\left( \xi _{ 0 } \right) }{ f\left( \infty \right) } \right) }^{ \Lambda \left( \mu \right) }\\ }$

ここで、

$\displaystyle { f\left( x \right) =\int _{ -\infty }^{ x }{ P_{ 1 }\left( h \right) dh } \\ f\left( \infty \right) =\int _{ -\infty }^{ \infty }{ P_{ 1 }\left( h \right) dh } =1 }$

であるため、

$\displaystyle { S\left( \xi _{ 0 },\mu \right) ={ \left( \frac { f\left( \xi _{ 0 } \right) }{ 1 } \right) }^{ \Lambda \left( \mu \right) }\\ ={ f\left( \xi _{ 0 } \right) }^{ \Lambda \left( \mu \right) }\\ }$

となります。これが高さ $\xi_0$ で $\mu$ の勾配でスタートしたときの遮蔽しない確率です。さて、ここから $G_{ 1 }^{ dist }$ は、光線の開始の高さがランダムでスタートするとしたら、高さ分布と遮蔽しない確率を畳み込んで、期待値を考えます。

$\displaystyle { G_{ 1 }^{ dist }\left( \mu \right) =\int _{ -\infty }^{ \infty }{ P_{ 1 }\left( h \right) S\left( \xi ,\mu \right) d\xi } \\ =\int _{ -\infty }^{ \infty }{ P_{ 1 }\left( \xi \right) { f\left( \xi \right) }^{ \Lambda \left( \mu \right) }d\xi } }$

ここで、

$\displaystyle { \int _{ -\infty }^{ \infty }{ P_{ 1 }\left( \xi \right) { f\left( \xi \right) }^{ \Lambda \left( \mu \right) }d\xi } \\ =\int _{ -\infty }^{ \infty }{ \dot { f } \left( \xi \right) { f\left( \xi \right) }^{ \Lambda \left( \mu \right) }d\xi } }$

また置換積分を実行して、

$\displaystyle { y=f\left( \xi \right) \\ \frac { dy }{ d\xi } =\dot { f } \left( \xi \right) d\xi \\ dy=\dot { f } \left( \xi \right) d\xi \\ \frac { dy }{ \dot { f } \left( \xi \right) } =d\xi \\ =\int _{ f\left( -\infty \right) }^{ f\left( \infty \right) }{ \dot { f } \left( \xi \right) { y }^{ \Lambda \left( \mu \right) }\frac { dy }{ \dot { f } \left( \xi \right) } } \\ =\int _{ 0 }^{ 1 }{ { y }^{ \Lambda \left( \mu \right) }dy } \\ =\left[ \frac { 1 }{ \Lambda \left( \mu \right) +1 } y^{ \Lambda \left( \mu \right) +1 } \right] ^{ 1 }_{ 0 }\\ =\frac { 1 }{ \Lambda \left( \mu \right) +1 } 1^{ \Lambda \left( \mu \right) +1 }-\frac { 1 }{ \Lambda \left( \mu \right) +1 } 0^{ \Lambda \left( \mu \right) +1 }\\ =\frac { 1 }{ \Lambda \left( \mu \right) +1 } }$

結果、

$\displaystyle { \Lambda \left( \mu \right) =\frac { 1 }{ \mu } \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } \\ G_{ 1 }^{ dist }\left( \mu \right) =\frac { 1 }{ \Lambda \left( \mu \right) +1 } }$

として、良く知られた、片方向 Smith shadow masking function が得られました。

ここでさらに、両方向の遮蔽を考えてみると、単純にSを二回やれば良さそうです。

$\displaystyle { G_{ 2 }^{ dist }\left( \mu _{ 1 },\mu _{ 2 } \right) =\int _{ -\infty }^{ \infty }{ P_{ 1 }\left( h \right) S\left( \xi ,\mu _{ 1 } \right) S\left( \xi ,\mu _{ 2 } \right) d\xi } }$

これは結局、先ほどと同様の流れで、

$\displaystyle { \\ \int _{ -\infty }^{ \infty }{ P_{ 1 }\left( h \right) S\left( \xi ,\mu _{ 1 } \right) S\left( \xi ,\mu _{ 2 } \right) d\xi } \\ =\int _{ -\infty }^{ \infty }{ \dot { f } \left( \xi \right) { f\left( \xi \right) }^{ \Lambda \left( \mu _{ 1 } \right) }{ f\left( \xi \right) }^{ \Lambda \left( \mu _{ 2 } \right) }d\xi } \\ =\int _{ -\infty }^{ \infty }{ \dot { f } \left( \xi \right) { f\left( \xi \right) }^{ \Lambda \left( \mu _{ 1 } \right) +\Lambda \left( \mu _{ 2 } \right) }d\xi } }$

となるので、あとはもう完全に同じのため、

$\displaystyle { G_{ 2 }^{ dist }\left( \mu _{ 1 },\mu _{ 2 } \right) =\frac { 1 }{ \Lambda \left( \mu _{ 1 } \right) +\Lambda \left( \mu _{ 2 } \right) +1 } }$

となります。これで最終的には、

$\displaystyle { G_{ 2 }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { \chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) \chi ^{ + }\left( \omega _{ i }\cdot \omega _{ m } \right) }{ \Lambda \left( \omega _{ o } \right) +\Lambda \left( \omega _{ i } \right) +1 } }$

※ $\mu$ は $\omega_o, \omega_i$ から求めることができます。

と、よく知られた height correlated Smith shadowing/masking を得ることができました。この導出はa raytracing formulationとも呼ばれています。しかしながら、この導出は直観的ではあるものの、この導出で厳密なGが得られているのか？という疑問はわずかに残ります。ただ実は片方向 Smith shadow masking function ならば、厳密に数式のみで解析的に導出することができ、 Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs"の "AppendixA. Derivation of the Masking Function" の部分に導出が乗っています。一応追いかければ同じ結果が得られるのですが、長い数式がつらつらと続いてしまうため、ここでは紹介にとどめます。

だんだん記事の編集が重くなってきたので、こぼれてしまった部分を Microfacet入門（２）として続きます。

参考文献

Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs"

Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces"

Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-scattering microfacet BSDFs with the Smith model"

Earl Hammon, Jr, GDC, "PBR Diffuse Lighting for GGX+Smith Microsurfaces"

Microfacetモデルの重点サンプリング

脱・完全鏡面反射～GGXについて調べてみた～

鏡面BRDF

島です！

レイトレ検定

三葉レイちゃんの応援メッセージ

セミナー

発表

シーンについて

イルカ

波

リング

クロス

床

部屋から見えた夕日

概要

[Kelemen 2001] のアプローチ

スペキュラ反射能

マット項

フレネル項

と のベイク

[Kelemen 2001] の近似について

実装

重点サンプリング

ベイクするときに誘導体フレネルを含んだ場合

導体想定の、ベイクするときにフレネル項を含まなかった場合

組み合わせる場合の確率密度

の重点サンプリング

実装例

White Furnace Test

"Multiple-Scattering Microfacet BSDFs with the Smith Model" との比較

多重拡散項の近似

まとめ

参考画像

導体

誘導体

参考文献

概要

単純な方法

Marsagliaの方法

A. 単位球面に対してランダム生成された点 は、それぞれ単一の軸にだけ着目すると-1~+1で密度は均一である

B. 単位円に対してランダム生成された点 (a, b) の は0~1で密度は均一である

組み合わせる

プログラミング

乱数生成回数の期待値

半球の場合

参考文献

スロープ空間

スロープ空間とヤコビアン

具体的なP

P2

Λ （Beckmann分布）

Λ （GGX分布）

実装例

まとめ

参考文献

動機

Microfacet

投影面積

マイクロサーフェスと立体角

マイクロサーフェス上の積分から、立体角上の積分へ

幾何学平面への投影

出射方向の投射面積

マスキング関数は一意に定まるか？

放射輝度

マイクロBRDF

抜け落ちた遮蔽

マイクロBRDF

変数変換

マイクロBRDF その2

エネルギー保存とマスキング関数

Gの中身, Smithモデル

Smithモデル の導出

参考文献

$a_{ spec }^{ avg }$ と $a_{ spec }\left( \theta \right)$ のベイク

$f_{ r,matte }$ の重点サンプリング

A. 単位球面に対してランダム生成された点は、それぞれ単一の軸にだけ着目すると-1~+1で密度は均一である

B. 単位円に対してランダム生成された点 (a, b) の $a^2+b^2$ は0~1で密度は均一である

Smithモデルの導出