Microfacet入門（１） - ushiostarfish’s diary

動機

現在リアルタイムレンダリング、およびオフラインレンダリングにて、マイクロファセット理論をベースにした材質の表現は幅広く使われています。また、それらをベースにした発展手法も数多く存在し、それらを追いかけていく上でも基礎理論を整理しておくことは重要のように思われます。しかしながら、マイクロファセットベースのBRDF&BSDFによく使われる式そのものの情報は数多くあるにも関わらず、それらの導出の部分に関する資料はかなり少ないように思いました。そこで本稿ではマイクロファセット理論に関する論文である、

Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs"

Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces"

をベースに紐解いていくことを目標にしようと思います。ただ、基本的には前者を追いかけるような形になります。ただ省略している部分もありますので、原著をあたっていただくと、どこが省略されているのかが丸見えになるので、合わせて参照していただくのが良いと思います。

Microfacet

マイクロファセット理論では、まず反射の複雑なふるまいは物体表面の微小な法線の分布によって起こると仮定しています。そこで何かしら基準となる空間を設けたいところです。慣習的には、面積が1である幾何学平面(geometric surface) を基準に、そこに凸凹したマイクロサーフェス(microsurface)を配置したモデルを使います。

f:id:ushiostarfish:20180321173208p:plain

※ Figure 2. The geometric surface and the microsurface. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

$M$ はマイクロサーフェスの領域、 $\omega_g$ は幾何学平面の法線、 $p_m$ がマイクロサーフェス上の点、 $\omega_m$ その点の法線を表しています。

即座にわかるポイントとしては、多少なりともでこぼこしたマイクロサーフェスの面積は全部集めてくると１を超えてしまうということがわかります。

投影面積

ここでちょっと図のようなマイクロサーフェスから、ある方向 $\omega_o$ への出射放射輝度を考えてみます。

f:id:ushiostarfish:20180321201952p:plain ※ Figure 1. The outgoing radiance of surfaceMis the average of the radiances from each point of the surface, weighted by their projected-area fractions towards the outgoing direction. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

まずはM全域にわたって放射輝度を集める必要があるため、積分を以下のように考えます。

$\displaystyle { \int _{ M }^{ }{ projected\ area\left( p_{ m } \right) L\left( \omega _{ o },p_{ m } \right) dp_{ m } } }$

ここで放射輝度は"見えている面積の分"だけ集めるため、投射された面積を基準にする必要があります。ここで投射であるため、 $cos \theta$ 使いたくなりますが、わざわざprojected areaとしているのは、隣接するマイクロサーフェスに遮蔽されるようなケースもあるため、ここでは文字で記述されています。

しかしまだこれではマイクロサーフェス上の面積範囲で積分してしまっているので出射放射輝度にはなりませんので、出射放射輝度とするために、投影面積で割ることで平均放射輝度としてあげる必要があります。それを付け加えると、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { \int _{ M }^{ }{ projected\ area\left( p_{ m } \right) L\left( \omega _{ o },p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ projected\ area\left( p_{ m } \right) dp_{ m } } } }$

となります。この考察から、

隣接するマイクロサーフェスに遮蔽される
投影

といったところが後々キーポイントになるであろうともわかってきます。

マイクロサーフェスと立体角

ベースとなるマイクロサーフェスが定義できましたが、実際のところ今後更なる解析を進めていくにあたって、マイクロサーフェスを立体角ベースでも考えていけると便利です。そこで何らかの形でマイクロサーフェスと立体角を結び付けておく必要があります。そこで、立体角を与えたらマイクロサーフェスの面積が返ってくる（この場合単位は $m^2/sr$ になりますね）-そんな関数を定義します。

$\displaystyle { D\left( \omega \right) =\int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } }$

ここで $\omega _{ m }\left( p_{ m } \right)$ はある点の法線であり、 $\delta \left( \right)$ は次元が $1/sr$ のデルタ関数であり、法線が一致しているところにピークが存在しています。

なんだかニュアンスは分からなくはないような・・・？分からないような気がします。そこで、ここではある任意の立体角の範囲での積分を考えてみます。

$\displaystyle { \int _{ \Omega _{ Any } }^{ }{ D\left( \omega \right) d\omega } \\ =\int _{ \Omega _{ Any } }^{ }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } d\omega } \\ =\int _{ M }^{ }{ \int _{ \Omega _{ Any } }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) d\omega } dp_{ m } } }$

ここで、

$\displaystyle { \int _{ \Omega _{ Any } }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) d\omega } }$

の部分に着目すると、デルタ関数は単体での積分結果は、範囲に含まれていれば1、そうでなければ0になります。つまり、Dを立体角で積分すると、その立体角に収まるような法線を持つマイクロサーフェスの面積になる、ということになります。このようにつじつまが合うように考えられた定義である、ということです。

もちろん全立体角の積分は、マイクロサーフェス全体の面積に一致します。

$\displaystyle { microsurface\ area=\int _{ M }^{ }{ dp_{ m } } =\int _{ \Omega }^{ }{ D\left( \omega _{ m } \right) d\omega _{ m } } }$

マイクロサーフェス上の積分から、立体角上の積分へ

先の節の拡張として、マイクロサーフェス上の関数を考えた場合、それを立体角に持っていくとき、

$\displaystyle { \int _{ M }^{ }{ g\left( p_{ m } \right) dp_{ m } } =\int _{ \Omega }^{ }{ g\left( \omega _{ m } \right) D\left( \omega _{ m } \right) d\omega _{ m } } }$

を満たすような $g\left( p_{ m } \right)$ と $g\left( \omega _{ m } \right)$ の関係性はどういったものでしょうか？やや天下り的ですが、以下のように結びつけるとうまくいきます。

$\displaystyle { g\left( \omega \right) =\frac { \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) g\left( p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } } }$

これは D と gをそれぞれ代入していくと確認することができます。

$\displaystyle { \int _{ \Omega }^{ }{ g\left( \omega _{ m } \right) D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \frac { \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) g\left( p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } } \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) g\left( p_{ m } \right) dp_{ m } } d\omega _{ m } } \\ =\int _{ M }^{ }{ \int _{ \Omega }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) g\left( p_{ m } \right) dp_{ m } } d\omega _{ m } } \\ =\int _{ M }^{ }{ g\left( p_{ m } \right) d\omega _{ m } } }$

なるほど、確かにうまく定義したものです。

幾何学平面への投影

ここでもう一度先のマイクロサーフェスの図を確認してみます

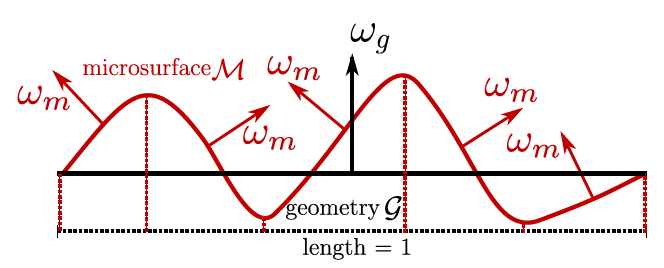f:id:ushiostarfish:20180321210211p:plain ※ Figure 3. (a) Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

マイクロサーフェス全体の面積は不明ですが、しかし幾何学平面gの面積は1にしていました。つまり、内積を使って幾何学平面に投射を考えてみると、以下の式が成り立つことがわかります。

$\displaystyle { \int _{ M }^{ }{ \omega _{ g }\cdot \omega _{ m }\left( p_{ m } \right) dp_{ m } } =1 }$

さらに、半球での積分を考えても、

$\displaystyle { \int _{ \Omega }^{ }{ \omega _{ g }\cdot \omega _{ m }D\left( \omega _{ m } \right) d\omega _{ m } } =1 }$

また同様のことを表している、ということになります。実際、具体的なD、たとえばBeckmann分布や、GGX分布を試しに数値積分してみると、確かに1になることを確認することもできます。

出射方向の投射面積

幾何学平面への投射ついでに、任意の出射方向への投射を一緒に考えておきましょう。まずは幾何学平面そのものの投射です。

f:id:ushiostarfish:20180324174447p:plain ※ Figure 3. (b) Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

幾何学平面の面積は1でした。したがって、その投射は当然 $\cos \theta$ および内積で表すことができます。

$\displaystyle { \int _{ \Omega }^{ }{ \omega _{ g }\cdot \omega _{ m }D\left( \omega _{ m } \right) d\omega _{ m } } =1 }$

ここでさらにマイクロサーフェスの投射を考えてみます。

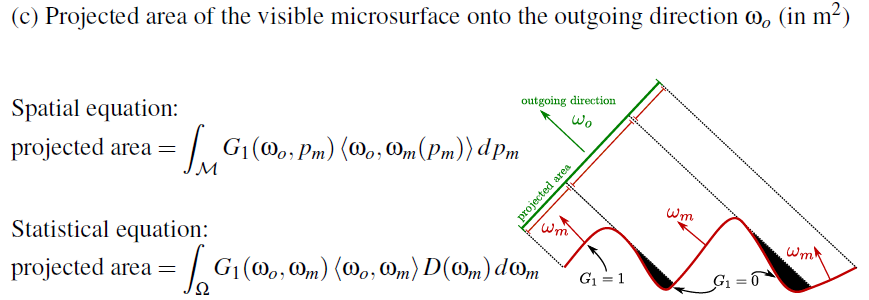f:id:ushiostarfish:20180324180225p:plain ※ Figure 3. (c) Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

$\lt \omega _{ o },\omega _{ m } \gt$ の部分は内積を正にクランプしたものを表しており、面積の投射を表現しています。つぎにGですが、空間ベース(Spatial) の方程式の $G_1\left( \omega_{ o },p_{ m } \right)$ はマイクロサーフェス上のある点が見えていれば1を、隠れていれば0 を返す関数です。一方、統計ベース(Statistical)の方程式の $G_1\left( \omega _{ o },\omega _{ m } \right)$ は、ある方向の法線を持つマイクロサーフェスのうち、何割が隠れているか？を表す関数です。尺度は違っていても、まったく同様の現象を表していることになります。

出射方向の投射面積の投射面積の表現の仕方が２種類あることがわかりました。そこで、投影面積の関係式が導かれます。

これがいわゆる単一方向のMasking Functionであり、具体的なGの内容を考える際には、この方程式を満たすかどうか？重要なポイントになってきます。ついでに、何割が隠れているか？というとちょっとふわっとしていたため、 $G_1\left( \omega _{ o },\omega _{ m } \right)$ を式として表現すると、マイクロサーフェス上の積分から、立体角上の積分への操作により、以下のように表現できます。

$\displaystyle { G_1\left( \omega _{ o },\omega _{ m } \right) =\frac { \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } } }$

※なんとなく、"遮蔽の割合"の意味が式から感じられる気がします

一応実際にこのバージョンでも確認してみると、

$\displaystyle { \cos { \theta _{ o } } =\int _{ \Omega }^{ }{ G_1\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \frac { \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } } \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \frac { \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } } \left< \omega _{ o },\omega _{ m } \right> \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) dp_{ m } } d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) dp_{ m } } \left< \omega _{ o },\omega _{ m } \right> d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \int _{ M }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) \left< \omega _{ o },\omega _{ m } \right> dp_{ m } } d\omega _{ m } } \\ =\int _{ M }^{ }{ \int _{ \Omega }^{ }{ \delta \left( \omega _{ m }\left( p_{ m } \right) \right) G_1\left( \omega _{ o },p_{ m } \right) \left< \omega _{ o },\omega _{ m } \right> d\omega _{ m } } dp_{ m } } \\ =\int _{ M }^{ }{ G_1\left( \omega _{ o },p_{ m } \right) \left< \omega _{ o },\omega _{ m } \right> dp_{ m } } }$

確かになりました。

マスキング関数は一意に定まるか？

先の投影面積の関係式、

と、任意のDがあれば、Gは一意に定まるんでしょうか？定まるとしたら、便利です。しかし実際は定まりません。以下の図を見てみましょう。

f:id:ushiostarfish:20180324200455p:plain ※ Figure 4. Microsurfaces with the same distribution of normals but with different profiles result in different BRDFs. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

図では法線分布が同じ２つの表面を比較しています。例えば赤が完全に隠れていたり、完全に見えたりしています。つまり表面の構造(論文中ではthe microsurface profileと呼ばれています)によって性質が異なってきてしまうのです。これは何を意味するかというと、Gを考えるときには、

"なんらかの仮定して、Gを導出する"

というプロセスが必要ということになります。このプロセスの違いが SmithのモデルだったりV-cavityだったりなどするということです。

放射輝度

最初に提示していたマイクロサーフェスからの放射輝度をもう一度見てみると、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { \int _{ M }^{ }{ projectedarea\left( p_{ m } \right) L\left( \omega _{ o },p_{ m } \right) dp_{ m } } }{ \int _{ M }^{ }{ projectedarea\left( p_{ m } \right) dp_{ m } } } }$

すでにいくつかの考察により、既知の量があり、それに乗り換えてみます。まずは分母の投影面積は、 $\cos \theta$ だったので、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { 1 }{ \cos { \theta _{ o } } } \int _{ M }^{ }{ projectedarea\left( p_{ m } \right) L\left( \omega _{ o },p_{ m } \right) dp_{ m } } }$

見えているところだけの放射輝度を反映するGと、投影を表す内積を組み込むと、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { 1 }{ \cos { \theta _{ o } } } \int _{ M }^{ }{ L\left( \omega _{ o },p_{ m } \right) G_1\left( \omega _{ o },p_{ m } \right) \left< \omega _{ o },\omega _{ m } \right> dp_{ m } } }$

これを統計ベース(Statistical)の方程式にもっていけば、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { 1 }{ \cos { \theta _{ o } } } \int _{ \Omega }^{ }{ L\left( \omega _{ o },\omega_{ m } \right) G_1\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } }$

だいぶ扱いやすい式になってきました。ここでさらにL以外をまとめ上げ、ここに "distribution of visible normals" (可視法線分布）と名前を付けます。

$\displaystyle { D_{ \omega }\left( \omega _{ m } \right) =\frac { G_1\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) }{ \cos { \theta _{ o } } } }$

すると先の式はそれに伴って、

$\displaystyle { L\left( \omega _{ o },M \right) =\frac { 1 }{ \cos { \theta _{ o } } } \int _{ \Omega }^{ }{ L\left( \omega _{ o },\omega_{ m } \right) G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ L\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ L\left( \omega _{ o },\omega_{ m } \right) D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } }$

こうすると、出射放射輝度はこの"distribution of visible normals" (可視法線分布）に重みづけされた平均であるという見方ができます。なにやらこじつけで無理やり名前を付けたようにも見えなくありませんが、"distribution "（分布）というからには、この新しい $D_{\omega}$ はちゃんと正規化されています。それはつまり、

$\displaystyle { \int _{ \Omega }^{ }{ D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } =1 }$

という意味です。だからこそ"出射放射輝度は可視法線分布により重みづけされた平均だ"という捉え方は、的を射ているといえます。これは以下のように確認することができます。

$\displaystyle { \int _{ \Omega }^{ }{ D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } =\int _{ \Omega }^{ }{ \frac { G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) }{ \cos { \theta _{ o } } } d\omega _{ m } } \\ =\frac { 1 }{ \cos { \theta _{ o } } } \int _{ \Omega }^{ }{ G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\frac { \int _{ \Omega }^{ }{ G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } }{ \int _{ \Omega }^{ }{ G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } } \\ =1 }$

マイクロBRDF

今まではマイクロサーフェスからの放射輝度だけを考えてきました。ただ実際にはマイクロサーフェスもなんらかの反射特性を有しており、入射と出射にはやはりその性質を考える必要があります。そこで、マイクロサーフェスのそれぞれの微小面のミクロの世界のBRDFを以下のように名前を付けることにします。

$\displaystyle { \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) }$

すると、微小面からの出射放射輝度は、レンダリング方程式から、

$\displaystyle { L\left( \omega _{ o },\omega _{ m } \right) =\int _{ \Omega _{ i } }^{ }{ \frac { dL\left( \omega _{ o },\omega _{ m } \right) }{ d\omega _{ i } } d\omega _{ i } } \\ L\left( \omega _{ o },\omega _{ m } \right) =\int _{ \Omega _{ i } }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> L\left( \omega _{ i } \right) d\omega _{ i } } }$

マクロな世界、マイクロサーフェスの出射放射輝度は、可視法線分布に重みづけされた平均だったので、

$\displaystyle { L\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ L\left( \omega _{ o },\omega _{ m } \right) D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } }$

ここで微小立体角の入射あたりの出射放射輝度の寄与を考えてみます

$\displaystyle { dL\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ dL\left( \omega _{ o },\omega _{ m } \right) D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } }$

これはやはり微小面からの出射放射輝度を考えればいいので、

$\displaystyle { dL\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> L\left( \omega _{ i } \right) D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } \\ =L\left( \omega _{ i } \right) \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } }$

これを一度積分形式に戻ると、

$\displaystyle { L\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \left( \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } \right) d\omega _{ m } } }$

となり、さらにマクロBRDF ( $\rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right)$ ) は一般に、

$\displaystyle { L\left( \omega _{ o },M \right) =\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \cos { \theta _{ i } } d\omega _{ m } } }$

であることを考え、 $D_\omega$ を展開しながら整理すると、

$\displaystyle { L\left( \omega _{ i } \right) \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \cos { \theta _{ i } } =L\left( \omega _{ i } \right) \left( \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } \right) \\ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \cos { \theta _{ i } } =\int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } \\ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { 1 }{ \cos { \theta _{ i } } } \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> D_{ \omega }\left( \omega _{ m } \right) d\omega _{ m } } \\ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { 1 }{ \cos { \theta _{ i } } } \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> \frac { G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) }{ \cos { \theta _{ o } } } d\omega _{ m } } \\ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { 1 }{ \cos { \theta _{ i } } \cos { \theta _{ o } } } \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } }$

と整理でき、またついでに内積を使った表現では、

とすることもできますね。だいぶBRDFの詳細が見えてきました。

抜け落ちた遮蔽

先の節で、定式化ができたように感じてしまいますが、抜け落ちてしまっているところがあります。一つは $G_1 \left( \omega_o, \omega_m \right)$ です。ここではoなので、出ていくときの遮蔽を考慮に入れています。しかしながら入射はどうか？というと考慮できていません。これはoをiにしても同様の問題が起きます。つまるところ実際には両方の遮蔽を考慮しないと変なわけです。これについてはいったんメモでとどめ、後ほど再び議論します。

マイクロBRDF

Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" では、マイクロBRDFを二つのケースを紹介しています。一つは完全拡散面、もう一つは完全鏡面です。ここでは完全鏡面を仮定して、BRDFを具体化していきます。

完全鏡面を表現するのにはやはりデルタ関数を使ってモデル化するのが良さそうです。例えば試しに完全鏡面のBRDFを考えるとき、直感的に、二つのベクトルが完全に反射の関係性を満たすところにピークのあるデルタ関数 $\delta \left( \omega _{ h },\omega _{ n } \right)$ をそのまま使ってみますと、

$\displaystyle { \rho _{ mirror }\left( \omega _{ o },\omega _{ i },\omega _{ n } \right) =\delta \left( \frac { \omega _{ o }+\omega _{ i } }{ \left\| \omega _{ o }+\omega _{ i } \right\| } ,\omega _{ n } \right) =\delta \left( \omega _{ h },\omega _{ n } \right) }$

しかし、実はこれは問題があり、レンダリング方程式に入れてみると、

$\displaystyle { L_{ o }=\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \rho _{ mirror }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \cos { \theta _{ i } } d\omega _{ i } } \\ =\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \delta \left( \omega _{ h },\omega _{ n } \right) \cos { \theta _{ i } } d\omega _{ i } } \\ =L\left( \omega _{ reflect } \right) \cos { \theta _{ i } } }$

これは見るからにおかしいです。つまり正しくはデルタ関数をそのまま使うのではなく、なんらかの補正係数が必要だったわけです。したがって、正しくは以下のように補正項をつけます。

$\displaystyle { \rho _{ mirror }\left( \omega _{ o },\omega _{ i },\omega _{ n } \right) =\frac { \delta \left( \omega _{ h },\omega _{ n } \right) }{ \cos { \theta _{ i } } } \\ L_{ o }=\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \rho _{ mirror }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \cos { \theta _{ i } } d\omega _{ i } } \\ =\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \frac { \delta \left( \omega _{ h },\omega _{ n } \right) }{ \cos { \theta _{ i } } } \cos { \theta _{ i } } d\omega _{ i } } \\ =\int _{ \Omega }^{ }{ L\left( \omega _{ i } \right) \delta \left( \omega _{ h },\omega _{ n } \right) d\omega _{ i } } \\ =L\left( \omega _{ reflect } \right) }$

これを踏まえ、先の式でマイクロBRDFはどのようになるのかを考えてみたいです。

$\displaystyle { \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { 1 }{ \left< \omega _{ i },\omega _{ g } \right> \left< \omega _{ i },\omega _{ g } \right> } \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } }$

しかし補正係数は今回自明ではないため、いったん k と置くことにします。

$\displaystyle { \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =k\delta \left( \omega _{ h },\omega _{ m } \right) }$

マイクロサーフェスとはいえ、通常のBRDFやBSDFと同様に、エネルギーは完全に保存されるはずなので、以下が成り立つはずです。

$\displaystyle { \int _{ \Omega _{ i } }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left| \omega _{ i }\cdot \omega _{ m } \right| d\omega _{ i } } =1\\ \int _{ \Omega _{ i } }^{ }{ k\delta \left( \omega _{ h },\delta \left( \omega _{ h } \right) \right) \left| \omega _{ i }\cdot \omega _{ m } \right| d\omega _{ i } } =1 }$

しかし困ったことに、デルタ関数の引数である $\omega _{ h }$ は積分の変数そのままではありません。したがって積分結果はいくばくかの補正がかかります。デルタ関数の引数に補正がかからないように変数変換を行いたくなってきます。

変数変換

先の要求を改めて確認すると、 $\omega _{ h }$ と、 $\omega _{ i }$ , $\omega _{ o }$ とを自由に変換できるようになりたい、というものでした。これには幾何学的関係性を考えることで係数が見えてきます。※ Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces"

まずは記号を整理します。

$\displaystyle { \vec { h } =\vec { i } +\vec { o } \\ \vec { h_{ r } } =\frac { \vec { h } }{ \left\| \vec { h } \right\| } }$

これはイメージとしては、

f:id:ushiostarfish:20180325181358p:plain

というようなかんじです。次に並べ替えて、

f:id:ushiostarfish:20180325181523p:plain

さらにハーフベクトルを書き込むと、

f:id:ushiostarfish:20180325181646p:plain

ここで、立体角 $\Delta \omega h$ と $\Delta \omega o$ の微小な関係性は、

$\displaystyle { \Delta \omega h=\left| \vec { o } \cdot \vec { h_{ r } } \right| \Delta \omega o }$

であり、さらに、

f:id:ushiostarfish:20180325182044p:plain

立体角 $\Delta \omega h_r$ と $\Delta \omega o$ の微小な関係性は、

$\displaystyle { \Delta \omega h_{ r }=\frac { \left| \vec { o } \cdot \vec { h_{ r } } \right| }{ { \left\| \vec { h } \right\| }^{ 2 } } \Delta \omega o }$

となり、さらに、hの長さを iとo、そしてhrを使って表すのをとっかかりにして、

$\displaystyle { \left\| \vec { h } \right\| =\left| \left( \vec { i } +\vec { o } \right) \cdot \vec { h_{ r } } \right| \\ =\left| \vec { i } \cdot \vec { h_{ r } } +\vec { o } \cdot \vec { h_{ r } } \right| \\ =\left| 2\vec { i } \cdot \vec { h_{ r } } \right| =\left| 2\vec { o } \cdot \vec { h_{ r } } \right| }$

となることから、

$\displaystyle { { \left\| \vec { h } \right\| }^{ 2 }={ \left| 2\vec { o } \cdot \vec { h_{ r } } \right| }^{ 2 }=4{ \left| \vec { o } \cdot \vec { h_{ r } } \right| }^{ 2 } }$

これを使って、

$\displaystyle { \Delta \omega h_{ r }=\frac { \left| \vec { o } \cdot \vec { h_{ r } } \right| }{ 4{ \left| \vec { o } \cdot \vec { h_{ r } } \right| }^{ 2 } } \Delta \omega o\\ \Delta \omega h_{ r }=\frac { 1 }{ 4\left| \vec { o } \cdot \vec { h_{ r } } \right| } \Delta \omega o }$

となるほど巧妙にも、幾何学的関係が明らかになりました。論文中ではヤコビアンの表記として以下のように表現されています。

$\displaystyle { \left\| \frac { \omega h_{ r } }{ \omega o } \right\| =\frac { 1 }{ 4\left| \vec { o } \cdot \vec { h_{ r } } \right| } }$

また屈折の場合も似たような感じで、以下のようにhを表して、微小な関係性を導くことができます。（※スネルの法則から屈折ベクトルの関係性を満たしていることを確認できます）

$\displaystyle { \vec { h } =-\eta _{ 1 }\vec { i } -\eta _{ 2 }\vec { o } }$

ただ今回は長くなってしまうのでいったんこの辺で割愛します。気になる方は、Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces" を直接参照していただけると良いと思います。

マイクロBRDF その2

さて、変数変換ができるようになったので、先の式、

を変数変換すると、

$\displaystyle { \int _{ \Omega _{ m } }^{ }{ k\delta \left( \omega _{ h },\delta \left( \omega _{ h } \right) \right) \left| \omega _{ i }\cdot \omega _{ m } \right| 4\left| \omega _{ i }\cdot \omega _{ h } \right| d\omega _{ m } } =1\\ \int _{ \Omega _{ m } }^{ }{ \delta \left( \omega _{ h },\delta \left( \omega _{ h } \right) \right) k4{ \left| \omega _{ i }\cdot \omega _{ h } \right| }^{ 2 }d\omega _{ m } } =1 }$

となり、mとhが一致しているので、簡単にデルタ関数を外すことができます。したがって、これを満たすkは、

$\displaystyle { k4{ \left| \omega _{ i }\cdot \omega _{ h } \right| }^{ 2 }=1\\ k=\frac { 1 }{ 4{ \left| \omega _{ i }\cdot \omega _{ h } \right| }^{ 2 } } }$

と求めることができ、さらにフレネル項を考慮してあげたマイクロBRDFは、以下のようになります。

$\displaystyle { \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\left\| \frac { \omega h }{ \omega i } \right\| \frac { F\left( \omega _{ o },\omega _{ h } \right) \delta \left( \omega _{ h },\omega _{ m } \right) }{ \left| \omega _{ i }\cdot \omega _{ h } \right| } =\frac { F\left( \omega _{ o },\omega _{ h } \right) \delta \left( \omega _{ h },\omega _{ m } \right) }{ 4{ \left| \omega _{ i }\cdot \omega _{ h } \right| }^{ 2 } } }$

これを先のマクロBRDFの式に代入して、hとmは同じものを表していることに注意しつつ整理すると、

$\displaystyle { \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { 1 }{ \left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \int _{ \Omega }^{ }{ \rho _{ M }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left< \omega _{ i },\omega _{ m } \right> G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\frac { 1 }{ \left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \int _{ \Omega }^{ }{ \frac { F\left( \omega _{ o },\omega _{ h } \right) \delta \left( \omega _{ h },\omega _{ m } \right) }{ 4{ \left| \omega _{ i }\cdot \omega _{ h } \right| }^{ 2 } } \left< \omega _{ i },\omega _{ m } \right> G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\frac { 1 }{ \left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \int _{ \Omega }^{ }{ \frac { F\left( \omega _{ o },\omega _{ h } \right) \delta \left( \omega _{ h },\omega _{ m } \right) }{ 4 } G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\frac { 1 }{ \left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \int _{ \Omega }^{ }{ \delta \left( \omega _{ h },\omega _{ m } \right) \frac { F\left( \omega _{ o },\omega _{ h } \right) G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) D\left( \omega _{ m } \right) }{ 4 } d\omega _{ m } } \\ =\frac { 1 }{ \left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \frac { F\left( \omega _{ o },\omega _{ h } \right) G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) D\left( \omega _{ m } \right) }{ 4 } \\ =\frac { F\left( \omega _{ o },\omega _{ h } \right) G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) D\left( \omega _{ m } \right) }{ 4\left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } }$

これが、良く知られたマイクロファセットベースのBRDFの形式です。(※Gが片側しか考慮していないことを除けば）

エネルギー保存とマスキング関数

BRDF, BSDFなどのエネルギー保存として以下の式がよく提示されます。

$\displaystyle { \int _{ \Omega _{ o } }^{ }{ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left| \omega _{ o }\cdot \omega _{ g } \right| d\omega _{ o } } \le 1\forall \omega _{ i } }$

完全にエネルギーが保存される場合は、

$\displaystyle { \int _{ \Omega _{ o } }^{ }{ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left| \omega _{ o }\cdot \omega _{ g } \right| d\omega _{ o } } = 1\forall \omega _{ i } }$

これはなんだったかといえば、例えば放射照度1が観測されたとして、その時の放射発散度を積分で求めていると解釈することができ、それはやはり同じく1である、というふうに考えると自然です。

そしてここでヘルムホルツ（Helmoholtz）の相反性を考えると、やはりiとoを逆転されても成り立つはずで、

$\displaystyle { \int _{ \Omega _{ i } }^{ }{ \rho \left( \omega _{ o },\omega _{ i },\omega _{ m } \right) \left| \omega _{ i }\cdot \omega _{ g } \right| d\omega _{ i } } =1\forall \omega _{ o } }$

とも良く書かれます。これは見方を変えると、全方位で周囲から来る放射輝度が1であったとき、どの方向への出射放射輝度も1である、という解釈ができます。この性質を数値積分によって確かめるテストを、"White Furnace Test"と呼びます。

では先のBRDFはどうか？というのを考えてみると、フレネル項を除けば、満たすことができます。なぜなら表面はマイクロサーフェスは完全鏡面を仮定しており、吸収されることははなから前提に存在しないためです。

$\displaystyle { \int _{ \Omega _{ i } }^{ }{ \frac { G_{ 1 }\left( \omega _{ h },\omega _{ o } \right) D\left( \omega _{ h } \right) }{ 4\left| \omega _{ i },\omega _{ g } \right| \left| \omega _{ o },\omega _{ g } \right| } \left| \omega _{ i }\cdot \omega _{ g } \right| d\omega _{ i } } =1\forall \omega _{ o }\\ \int _{ \Omega _{ i } }^{ }{ \frac { G_{ 1 }\left( \omega _{ h },\omega _{ o } \right) D\left( \omega _{ h } \right) }{ 4\left| \omega _{ o },\omega _{ g } \right| } d\omega _{ i } } =1\forall \omega _{ o } }$

しかし、これはちょうど以下の図のような状況です。

f:id:ushiostarfish:20180325221717p:plain ※ Figure 6. (b) Normalization of specular microfacet-based BRDFs. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

もしかすると、iとoを逆にしたほうが図としっくりくるかもしれません。

$\displaystyle { \int _{ \Omega _{ o } }^{ }{ \frac { G_{ 1 }\left( \omega _{ h },\omega _{ i } \right) D\left( \omega _{ h } \right) }{ 4\left| \omega _{ i },\omega _{ g } \right| } d\omega _{ o } } =1\forall \omega _{ i } }$

図では完全にマイクロサーフェス上をエネルギーが突き抜けてしまっています。これはなぜかといえば、単方向しか遮蔽を考慮できておらず、最後の式では出射に対して遮蔽がありません。そこで両方向遮蔽を考慮した $G_2$ が都合よく見つかったと仮定して考えてみましょう。

$\displaystyle { \int _{ \Omega _{ o } }^{ }{ \frac { G_{ 2 }\left( \omega _{ h },\omega _{ i },\omega _{ o } \right) D\left( \omega _{ h } \right) }{ 4\left| \omega _{ i },\omega _{ g } \right| } d\omega _{ o } } }$

・・・これは当然ですがエネルギーが失われます。

これを表しているのが以下の図です。

f:id:ushiostarfish:20180325223603p:plain ※ Figure 6. (c) Normalization of specular microfacet-based BRDFs. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

しかしマイクロサーフェス上は完全鏡面を仮定したにもかかわらず、エネルギーが失われることは、極めて不自然です。なぜエネルギーが失われたかといえば、遮蔽された部分を0にしているからで、本来なら遮蔽されたとしても、そこからまた反射を繰り返し、どこかでは必ず外へ出ていくはずです。これは多重拡散をなんらかの形で考慮しなければ、エネルギーを保存させることが難しいことを示唆しています。これを表したのが以下の図です。

f:id:ushiostarfish:20180325224114p:plain ※ Figure 6. (d) Normalization of specular microfacet-based BRDFs. Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" より

Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" ではこれに対する解決策は提示されていませんが、しかし後の 2016年に、

Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-scattering microfacet BSDFs with the Smith model"

の論文が発表され、この多重拡散部分も解析的にモデル化することに成功しています。

f:id:ushiostarfish:20180325224649p:plain Figure 16: White furnace test for different microfacet materials. Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-scattering microfacet BSDFs with the Smith model" より

こちらは完全に本稿の範囲を超えてしまう上、自分のレベルではまだ理解できていないため、紹介にとどめることにいたします。

話を戻しますが、遮蔽を一部無視する形であれ、不完全でありながらもエネルギーの保存を確認することのできる、

のテストはそれなりに便利であり、これを論文中では、"Weak White Furnace Test"と呼んでいます。ただし、これは片方向での遮蔽のみでBRDFを設計することを勧めているわけではないことは注意が必要です。

Gの中身, Smithモデル

今までGの中身についてはあまり議論してきませんでした。枠組みがだいぶできてきたので、そろそろ中身に踏み込んでいきます。マスキング関数は一意に定まるか？の節で、Gを考えるときには、なんらかの仮定が必要という話をしました。スミスモデルの重要な仮定は、

・ミクロな表面の高さと向きは、無相関である

というところです。以下の図の右のような状態です。

f:id:ushiostarfish:20180331193214p:plain Figure 7. Microsurfaces and their autocorrelation functions. (left) A real-world continuous microsurface with large autocorrelation distance. (right) A uncorrelated surface, where each microfacet is not correlated to its neighborhood, as Smith models. Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-scattering microfacet BSDFs with the Smith model" より

なんだかそんな表面あり得るのか？という気もしないでもありませんが、このおかげで G を以下のように二つの関数に分離することができます。

$\displaystyle { G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) =G_{ 1 }^{ local }\left( \omega _{ o },\omega _{ m } \right) G_{ 1 }^{ dist }\left( \omega _{ o } \right) }$

$G_{ 1 }^{ local }\left( \omega _{ o },\omega _{ m } \right)$ は、出射に対して表面が見えているか？という角度に対する関数で、 $G_{ 1 }^{ dist }\left( \omega _{ o } \right)$ は、別の表面にどの程度遮蔽されているか？という関数です。こちらは遮蔽ですので、どうやらミクロな表面の高さ分布によって決まりそうです。

なぜ分離できるんでしょうか？例えば、ミクロな表面の高さと角度になんらかの関係性があり、例えば以下のような分布をしているとします。

f:id:ushiostarfish:20180331201915p:plain

ちょうど条件付き確率のような構造です。これでは、例えば高さ h > 3 であり、かつ 60 <= θ <= 90 であるミクロサーフェスが全体のどの程度を占めるのかを考えたいとき、 hに依存してθの分布を考えたりなど、相互の関係性を考慮にいれなければ、正しく求められません。しかし仮に相互に相関がない場合は、例えば以下のような図の状態です。

f:id:ushiostarfish:20180331201847p:plain

完全に格子状になっていますね、これなら、例えば高さ h > 3 であり、かつ 60 <= θ <= 90 であるミクロサーフェスが全体のどの程度を占めるのか？は、個別に関数を考えて、その積で表すことができる、ということです。

中身の話に移ると、まず、 $G_{ 1 }^{ local }\left( \omega _{ o },\omega _{ m } \right)$ は "local masking function" と呼ばれ、出射に対して表面が見えているか？という関数だったので、

$\displaystyle { G_{ 1 }^{ local }\left( \omega _{ o },\omega _{ m } \right) =\chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) }$

で表されます。ここで $\chi^+ \left( x \right)$ は、ヘヴィサイドの階段関数であり、以下のような関数です

f:id:ushiostarfish:20180331203305p:plain

※ ヘヴィサイドの階段関数 - Wikipedia より

平たい話、出射に対して表面が見えていれば 1 ,裏返って見えていなければ0 というわけです。

では、 $G_{ 1 }^{ dist }\left( \omega _{ o } \right)$ は、別の表面にどの程度遮蔽されているか？という関数だと述べましたが、この関数は未知の関数です。しかしながら、出射方向の投射面積で述べた、投影面積の関係式、

に Gの具体的な形を代入してみると、

$\displaystyle { \cos { \theta _{ o } } =\int _{ \Omega }^{ }{ G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ G_{ 1 }^{ local }\left( \omega _{ o },\omega _{ m } \right) G_{ 1 }^{ dist }\left( \omega _{ o } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =\int _{ \Omega }^{ }{ \chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) G_{ 1 }^{ dist }\left( \omega _{ o } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ =G_{ 1 }^{ dist }\left( \omega _{ o } \right) \int _{ \Omega }^{ }{ \chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } \\ G_{ 1 }^{ dist }\left( \omega _{ o } \right) =\frac { \cos { \theta _{ o } } }{ \int _{ \Omega }^{ }{ \chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } } }$

と導かれ、したがって、

$\displaystyle { G_{ 1 }\left( \omega _{ o },\omega _{ m } \right) =\chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) \frac { \cos { \theta _{ o } } }{ \int _{ \Omega }^{ }{ \chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) \left< \omega _{ o },\omega _{ m } \right> D\left( \omega _{ m } \right) d\omega _{ m } } } }$

と、Dの具体的な形が定まれば、Gは確かに自動的に定まるようになりました。ただ実際これをBRDFなどで使おうと思うと、解析的に式内の積分が解けないケースでは、評価のたびにこの積分を数値的に評価をしなければならず、非効率です。そのため事前計算を行い、テーブルに格納しておくなどの工夫を余儀なくされます。そこで、次のパートでは、現在広く使われている、SmithモデルではGをどのように扱っているのか？を考えていきます。

Smithモデルの導出

Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces" および、Earl Hammon, Jr, GDC, "PBR Diffuse Lighting for GGX+Smith Microsurfaces" の151ページ~157ページによると、Smithモデルにおいては、ミクロな表面からの光線を追跡する考え方で、Gを求める方法が紹介されています。

以下の図が概念図です。 f:id:ushiostarfish:20180331205923p:plain

※Figure 16: Geometry for Smith shadowing-masking G1 for direction v, corresponding to a visibility ray has starting height ξ0 and slope μ. At distance τ (measured along macrosurface), the microsurface has height ξ and slope q. Bruce Walter, Stephen R. Marschner, Hongsong Li, Kenneth E. Torrance, "Microfacet Models for Refraction through Rough Surfaces"より ※ 概念図であるため、ミクロな表面はつながって描かれています。 ※ 概念図は一次元的ですが、等方的なDを考える場合はどのように１次元に切り取っても同じであるため、一次元で考えます。

大変ごちゃごちゃしていますが、あるミクロ表面の高さ $\xi_0$ の場所から角度 $\theta _v$ の角度で横方向に $\tau$ だけ進んでいる状況で、その時のミクロ表面の高さが $\xi$ であり、さらにもうちょっと $\Delta \tau$ だけ進むところの図です。 $q$ は、横方向に $\tau$ 進んだときのミクロ表面の勾配で、 $\mu$ は光線の勾配です。

もうちょっと $\Delta \tau$ だけ進む、という状況について考えてみます。

$\mu$ については、 $\theta_v$ から、

$\displaystyle { \mu =\left| \tan { \left( \frac { \pi }{ 2 } -\theta _{ v } \right) } \right| =\left| \frac { 1 }{ \tan { \theta _{ v } } } \right| =\left| \cot \theta _{ v } \right| }$

となります。絶対値がついているのは、θのマイナスを考慮しているためです。

次に、ちょっと $\Delta \tau$ だけ進んだときにミクロ表面に衝突するための条件は、高さに着目して、進む前にぶつかっていない、つまり、

$\displaystyle { \xi _{ 0 }+\mu \tau >\xi }$

であり、かつ進んだときにぶつかる、

$\displaystyle { \xi _{ 0 }+\mu \tau +\mu \Delta \tau <\xi +q\Delta }$

※Earl Hammon, Jr, GDC, "PBR Diffuse Lighting for GGX+Smith Microsurfaces" では、この式の不等号の向きが逆です。これはタイポだと思われます。

この二つの条件が必要であり、二つ目の式を整理すると、

$\displaystyle { \xi _{ 0 }+\mu \tau +\mu \Delta \tau <\xi +q\Delta \tau \\ \xi _{ 0 }+\mu \tau +\mu \Delta \tau -q\Delta \tau <\xi \\ \xi >\xi _{ 0 }+\mu \tau +\mu \Delta \tau -q\Delta \tau }$

となり、二つをくっつけると、

$\displaystyle { \xi _{ 0 }+\mu \tau >\xi >\xi _{ 0 }+\mu \tau +\mu \Delta \tau -q\Delta \tau \\ \xi _{ 0 }+\mu \tau >\xi >\xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }$

このことから、

$\displaystyle { -\left( q-\mu \right) \Delta \tau <0\\ -\left( q-\mu \right) <0\\ q-\mu >0\\ q>\mu }$

であることがわかります。これが、ちょっと $\Delta \tau$ だけ進んだときにミクロ表面に衝突するための条件、ということになります。

ここで高さ分布を表す関数を、

$\displaystyle { P_{ 1 }\left( h \right) }$

で表し、そしてこれは、分布なので、

$\displaystyle { \int _{ -\infty }^{ \infty }{ P_{ 1 }\left( h \right) dh } =1 }$

であります。また、単一方向へ（一次元の）の勾配分布関数を、

$\displaystyle { P_{ 2 }\left( q \right) }$

で表し、これは何かといえば、引数に $\tan \theta$ を入れると、ミクロ表面に $\theta$ を持つ分布が返ってくるという関数です。尺度が勾配であるだけで、実際にはDから機械的に求めます。その詳細はいったん省略しますが、後に詳しく議論します。この関数は既知である、ということを前提にして次に進みます。なぜこんな関数が必要なのかというと、先の概念図でのq をうまく扱うため、と言ってもよいかもしれません。

こちらも分布なので、

$\displaystyle { \int _{ \infty }^{ \infty }{ P_{ 2 }\left( q \right) dq } =1 }$

であり、さらに例えば、

$\displaystyle { -\theta \le q\le \theta }$

の範囲に角度をもつミクロな表面の全体からみた割合は、

$\displaystyle { \int _{ \tan { \left( -\theta \right) } }^{ \tan { \theta } }{ P_{ 2 }\left( q \right) dq } }$

で求められる、というわけです。

これを踏まえて、ちょっと $\Delta \tau$ だけ進んだときにミクロ表面に衝突する条件、

$\displaystyle { \xi _{ 0 }+\mu \tau >\xi >\xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }$

および、

$\displaystyle { q>\mu }$

から、ちょっと $\Delta \tau$ だけ進んだときにミクロ表面に衝突する確率は、この条件を満たすミクロ表面の割合と一致するはずです。したがって、その確率は、

$\displaystyle { \int _{ \mu }^{ \infty }{ \int _{ \xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) P_{ 2 }\left( q \right) dhdq } } \\ =\int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \int _{ \xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dhdq } } }$

ここで極限をとります。

$\displaystyle { \lim _{ \Delta \tau \rightarrow d\tau }{ \Delta \tau } =d\tau }$

すると右の部分は、

$\displaystyle { \lim _{ \Delta \tau \rightarrow d\tau }{ \int _{ \xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dh } } =P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \left\{ \left( \xi _{ 0 }+\mu \tau \right) -\left( \xi _{ 0 }+\mu \tau -\left( q-\mu \right) d\tau \right) \right\} \\ =P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \left( q-\mu \right) d\tau }$

したがって、確率は、

$\displaystyle { \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \int _{ \xi _{ 0 }+\mu \tau -\left( q-\mu \right) \Delta \tau }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dhdq } } =\int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \left( q-\mu \right) d\tau dq } \\ =d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }$

となります。しかし、このアイディアには抜けていることがあります。今までの議論は、暗黙に、 $\tau$ 進んだ時点で、高さ $\xi _{ 0 }+\mu \tau$ 以下にあらかじめ存在していなければならない点です。これは条件付き確率として考えることができ、Aの条件のもとBが起こる確率は、

$\displaystyle { P\left( B|A \right) =\frac { P\left( B\wedge A \right) }{ P\left( A \right) } }$

と表されます。先ほどまで考えていた、確率というのは、 $P\left( B\wedge A \right)$ の部分に相当するため、

$\displaystyle { P\left( A\wedge B \right) =d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }$

となり、 $P\left( A \right)$ は、

$\displaystyle { P\left( A \right) =\int _{ -\infty }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dh } }$

これをいったん $f$ とおきますと、

$\displaystyle { \int _{ -\infty }^{ x }{ P_{ 1 }\left( h \right) dh } =f\left( x \right) \\ \int _{ -\infty }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dh } =f\left( \xi _{ 0 }+\mu \tau \right) }$

すると、 $d\tau$ だけ進んだときにミクロ表面に衝突する確率は、

$\displaystyle { P\left( A|B \right) =\frac { d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }{ \int _{ -\infty }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dh } } \\ =\frac { d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }{ f\left( \xi _{ 0 }+\mu \tau \right) } }$

となるわけです。ようやく少し見えてはきましたが、あくまで $d\tau$ の増加分に対する衝突確率でした。これをなんとかして、ある $\xi$ から傾き $\mu$ で $\tau$ 進んだときの生き残り割合として以下のような関数に定式化したいと考えます。

$\displaystyle { S\left( \xi ,\mu ,\tau \right) }$

この関数は、 $\tau$ が進めば進むほど生き残る確率は下がっていきます。これを単純化して、 $x_0, x_1,...$ をステップごとの生存確率だとすると、何回かステップを進めたときの生存確率は、

$\displaystyle { S_{ 1 }=x_{ 1 }\\ S_{ 2 }=x_{ 2 }x_{ 1 }\\ S_{ 3 }=x_{ 3 }x_{ 2 }x_{ 1 }\\ S_{ 4 }=x_{ 4 }x_{ 3 }x_{ 2 }x_{ 1 } }$

のように１ステップごとの生存確率の積で表せます。ここで４ステップ目進めるときの部分に着目すると、

$\displaystyle { \Delta S_{ 4 }=S_{ 4 }-S_{ 3 }\\ =x_{ 4 }x_{ 3 }x_{ 2 }x_{ 1 }-x_{ 3 }x_{ 2 }x_{ 1 }\\ =x_{ 4 }S_{ 3 }-S_{ 3 } }$

これを任意の１ステップに抽象化して、

$\displaystyle { \Delta S_{ n }=x_{ n }S_{ n-1 }-S_{ n-1 }\\ \Delta S_{ n }=S_{ n-1 }\left( x_{ n }-1 \right) }$

ここで $x_n$ は、1-衝突確率であるので、

$\displaystyle { \Delta S_{ n }=S_{ n-1 }\left( 1-P_{ collision }-1 \right) \\ \Delta S_{ n }=-S_{ n-1 }P_{ collision } }$

結果衝突せずに生き残る確率の変化量は、最終的に、

$\displaystyle { dS=-\left( \frac { d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }{ f\left( \xi _{ 0 }+\mu \tau \right) } \right) S\\ \frac { dS }{ d\tau } =-\left( \frac { d\tau P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }{ f\left( \xi _{ 0 }+\mu \tau \right) } \right) S }$

となり、微分方程式の形でSを表すことができました。こうなると解きたくなってきます。いったん長いので、

$\displaystyle { g\left( \tau \right) =\frac { P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }{ f\left( \xi _{ 0 }+\mu \tau \right) } }$

と置くことにして、

$\displaystyle { \\ \dot { S } \left( x \right) =-g\left( x \right) S\left( x \right) \\ \frac { \dot { S } \left( x \right) }{ S\left( x \right) } =-g\left( x \right) \\ \int { \frac { \dot { S } \left( x \right) }{ S\left( x \right) } dx } =\int { -g\left( x \right) dx } +C }$

置換積分を実行して、

$\displaystyle { S\left( x \right) =y\\ \dot { S } \left( x \right) =\frac { dy }{ dx } \\ \dot { S } \left( x \right) dx=dy\\ dx=\frac { dy }{ \dot { S } \left( x \right) } \\ \int { \frac { 1 }{ y } dy } =\int { -g\left( x \right) dx } +C\\ \ln { \left( y \right) } =\int { -g\left( x \right) dx } +C\\ { e }^{ \int { -g\left( x \right) dx } +C }=y\\ { e }^{ \int { -g\left( x \right) dx } +C }=S\\ { e }^{ \int _{ 0 }^{ \tau }{ -g\left( x \right) dx } +C }=S\left( \tau \right) }$

積分定数は、

$\displaystyle { S\left( 0 \right) =1\\ { e }^{ C }=1\\ C=0 }$

したがって、

$\displaystyle { { e }^{ \int _{ 0 }^{ \tau }{ -g\left( x \right) dx } }=S\left( \tau \right) }$

ここで、gの積分をさらに考えていきます。

まず、

$\displaystyle { f\left( \xi _{ 0 }+\mu \tau \right) =\int _{ -\infty }^{ \xi _{ 0 }+\mu \tau }{ P_{ 1 }\left( h \right) dh } }$

に見やすく名前をつけて、

$\displaystyle { f\left( \xi _{ 0 }+\mu \tau \right) =f_{ \tau }\left( \tau \right) }$

これの微分は、

$\displaystyle { \dot { f_{ \tau } } \left( \tau \right) =\frac { d }{ d\tau } f\left( \xi _{ 0 }+\mu \tau \right) =\mu P_{ 1 }\left( \xi _{ 0 }+\mu \tau \right) }$

ここで、今筆者と読者に天啓が下ったとして、

$\displaystyle { \Lambda \left( \mu \right) =\frac { 1 }{ \mu } \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } }$

と置くと、

$\displaystyle { g\left( \tau \right) =\Lambda \left( \mu \right) \frac { \dot { f_{ \tau } } \left( \tau \right) }{ f_{ \tau }\left( \tau \right) } }$

となり、積分は、

$\displaystyle { \int _{ 0 }^{ \tau }{ g\left( t \right) d } t=\int _{ 0 }^{ \tau }{ \Lambda \left( \mu \right) \frac { \dot { f_{ \tau } } \left( t \right) }{ f_{ \tau }\left( t \right) } dt } }$

さらに置換積分で、

$\displaystyle { y=f_{ \tau }\left( t \right) \\ \frac { dy }{ dt } =\dot { f_{ \tau } } \left( t \right) \\ dy=dt\dot { f_{ \tau } } \left( t \right) \\ \frac { dy }{ \dot { f_{ \tau } } \left( t \right) } =dt\\ =\int _{ f_{ \tau }\left( 0 \right) }^{ f_{ \tau }\left( t \right) }{ \Lambda \left( \mu \right) \frac { 1 }{ y } dy } }$

あとは素直に、

$\displaystyle { =\left[ \Lambda \left( \mu \right) \ln { \left| y \right| } \right] ^{ f_{ \tau }\left( t \right) }_{ f_{ \tau }\left( 0 \right) }\\ =\left[ \Lambda \left( \mu \right) \ln { \left( y \right) } \right] ^{ f_{ \tau }\left( t \right) }_{ f_{ \tau }\left( 0 \right) }\\ =\Lambda \left( \mu \right) \ln { \left( f_{ \tau }\left( \tau \right) \right) } -\Lambda \left( \mu \right) \ln { \left( f_{ \tau }\left( 0 \right) \right) } \\ =\Lambda \left( \mu \right) \left\{ \ln { \left( f_{ \tau }\left( \tau \right) \right) } -\ln { \left( f_{ \tau }\left( 0 \right) \right) } \right\} \\ =\Lambda \left( \mu \right) \left\{ \ln { \left( f\left( \xi _{ 0 }+\mu \tau \right) \right) } -\ln { \left( f\left( \xi _{ 0 } \right) \right) } \right\} \\ =\Lambda \left( \mu \right) \ln { \left( \frac { f\left( \xi _{ 0 }+\mu \tau \right) }{ f\left( \xi _{ 0 } \right) } \right) } }$

以上をまとめると、

$\displaystyle { S\left( \xi _{ 0 },\mu ,\tau \right) ={ e }^{ \int _{ 0 }^{ \tau }{ -g\left( x \right) dx } }\\ ={ e }^{ -\Lambda \left( \mu \right) \ln { \left( \frac { f\left( \xi _{ 0 }+\mu \tau \right) }{ f\left( \xi _{ 0 } \right) } \right) } }\\ ={ \left( { e }^{ \ln { \left( \frac { f\left( \xi _{ 0 }+\mu \tau \right) }{ f\left( \xi _{ 0 } \right) } \right) } } \right) }^{ -\Lambda \left( \mu \right) }\\ ={ \left( \frac { f\left( \xi _{ 0 }+\mu \tau \right) }{ f\left( \xi _{ 0 } \right) } \right) }^{ -\Lambda \left( \mu \right) }\\ ={ \left( \frac { f\left( \xi _{ 0 } \right) }{ f\left( \xi _{ 0 }+\mu \tau \right) } \right) }^{ \Lambda \left( \mu \right) } }$

ただ実際には、 $\tau$ は、∞になるべき存在です。そこで、生存確率は、

$\displaystyle { S\left( \xi _{ 0 },\mu ,\tau \right) ={ \left( \frac { f\left( \xi _{ 0 } \right) }{ f\left( \xi _{ 0 }+\mu \tau \right) } \right) }^{ \Lambda \left( \mu \right) }\\ S\left( \xi _{ 0 },\mu \right) =\lim _{ \tau \rightarrow \infty }{ S\left( \xi _{ 0 },\mu ,\tau \right) } \\ ={ \left( \frac { f\left( \xi _{ 0 } \right) }{ f\left( \infty \right) } \right) }^{ \Lambda \left( \mu \right) }\\ }$

ここで、

$\displaystyle { f\left( x \right) =\int _{ -\infty }^{ x }{ P_{ 1 }\left( h \right) dh } \\ f\left( \infty \right) =\int _{ -\infty }^{ \infty }{ P_{ 1 }\left( h \right) dh } =1 }$

であるため、

$\displaystyle { S\left( \xi _{ 0 },\mu \right) ={ \left( \frac { f\left( \xi _{ 0 } \right) }{ 1 } \right) }^{ \Lambda \left( \mu \right) }\\ ={ f\left( \xi _{ 0 } \right) }^{ \Lambda \left( \mu \right) }\\ }$

となります。これが高さ $\xi_0$ で $\mu$ の勾配でスタートしたときの遮蔽しない確率です。さて、ここから $G_{ 1 }^{ dist }$ は、光線の開始の高さがランダムでスタートするとしたら、高さ分布と遮蔽しない確率を畳み込んで、期待値を考えます。

$\displaystyle { G_{ 1 }^{ dist }\left( \mu \right) =\int _{ -\infty }^{ \infty }{ P_{ 1 }\left( h \right) S\left( \xi ,\mu \right) d\xi } \\ =\int _{ -\infty }^{ \infty }{ P_{ 1 }\left( \xi \right) { f\left( \xi \right) }^{ \Lambda \left( \mu \right) }d\xi } }$

ここで、

$\displaystyle { \int _{ -\infty }^{ \infty }{ P_{ 1 }\left( \xi \right) { f\left( \xi \right) }^{ \Lambda \left( \mu \right) }d\xi } \\ =\int _{ -\infty }^{ \infty }{ \dot { f } \left( \xi \right) { f\left( \xi \right) }^{ \Lambda \left( \mu \right) }d\xi } }$

また置換積分を実行して、

$\displaystyle { y=f\left( \xi \right) \\ \frac { dy }{ d\xi } =\dot { f } \left( \xi \right) d\xi \\ dy=\dot { f } \left( \xi \right) d\xi \\ \frac { dy }{ \dot { f } \left( \xi \right) } =d\xi \\ =\int _{ f\left( -\infty \right) }^{ f\left( \infty \right) }{ \dot { f } \left( \xi \right) { y }^{ \Lambda \left( \mu \right) }\frac { dy }{ \dot { f } \left( \xi \right) } } \\ =\int _{ 0 }^{ 1 }{ { y }^{ \Lambda \left( \mu \right) }dy } \\ =\left[ \frac { 1 }{ \Lambda \left( \mu \right) +1 } y^{ \Lambda \left( \mu \right) +1 } \right] ^{ 1 }_{ 0 }\\ =\frac { 1 }{ \Lambda \left( \mu \right) +1 } 1^{ \Lambda \left( \mu \right) +1 }-\frac { 1 }{ \Lambda \left( \mu \right) +1 } 0^{ \Lambda \left( \mu \right) +1 }\\ =\frac { 1 }{ \Lambda \left( \mu \right) +1 } }$

結果、

$\displaystyle { \Lambda \left( \mu \right) =\frac { 1 }{ \mu } \int _{ \mu }^{ \infty }{ P_{ 2 }\left( q \right) \left( q-\mu \right) dq } \\ G_{ 1 }^{ dist }\left( \mu \right) =\frac { 1 }{ \Lambda \left( \mu \right) +1 } }$

として、良く知られた、片方向 Smith shadow masking function が得られました。

ここでさらに、両方向の遮蔽を考えてみると、単純にSを二回やれば良さそうです。

$\displaystyle { G_{ 2 }^{ dist }\left( \mu _{ 1 },\mu _{ 2 } \right) =\int _{ -\infty }^{ \infty }{ P_{ 1 }\left( h \right) S\left( \xi ,\mu _{ 1 } \right) S\left( \xi ,\mu _{ 2 } \right) d\xi } }$

これは結局、先ほどと同様の流れで、

$\displaystyle { \\ \int _{ -\infty }^{ \infty }{ P_{ 1 }\left( h \right) S\left( \xi ,\mu _{ 1 } \right) S\left( \xi ,\mu _{ 2 } \right) d\xi } \\ =\int _{ -\infty }^{ \infty }{ \dot { f } \left( \xi \right) { f\left( \xi \right) }^{ \Lambda \left( \mu _{ 1 } \right) }{ f\left( \xi \right) }^{ \Lambda \left( \mu _{ 2 } \right) }d\xi } \\ =\int _{ -\infty }^{ \infty }{ \dot { f } \left( \xi \right) { f\left( \xi \right) }^{ \Lambda \left( \mu _{ 1 } \right) +\Lambda \left( \mu _{ 2 } \right) }d\xi } }$

となるので、あとはもう完全に同じのため、

$\displaystyle { G_{ 2 }^{ dist }\left( \mu _{ 1 },\mu _{ 2 } \right) =\frac { 1 }{ \Lambda \left( \mu _{ 1 } \right) +\Lambda \left( \mu _{ 2 } \right) +1 } }$

となります。これで最終的には、

$\displaystyle { G_{ 2 }\left( \omega _{ o },\omega _{ i },\omega _{ m } \right) =\frac { \chi ^{ + }\left( \omega _{ o }\cdot \omega _{ m } \right) \chi ^{ + }\left( \omega _{ i }\cdot \omega _{ m } \right) }{ \Lambda \left( \omega _{ o } \right) +\Lambda \left( \omega _{ i } \right) +1 } }$

※ $\mu$ は $\omega_o, \omega_i$ から求めることができます。

と、よく知られた height correlated Smith shadowing/masking を得ることができました。この導出はa raytracing formulationとも呼ばれています。しかしながら、この導出は直観的ではあるものの、この導出で厳密なGが得られているのか？という疑問はわずかに残ります。ただ実は片方向 Smith shadow masking function ならば、厳密に数式のみで解析的に導出することができ、 Eric Heitz "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs"の "AppendixA. Derivation of the Masking Function" の部分に導出が乗っています。一応追いかければ同じ結果が得られるのですが、長い数式がつらつらと続いてしまうため、ここでは紹介にとどめます。

だんだん記事の編集が重くなってきたので、こぼれてしまった部分を Microfacet入門（２）として続きます。